题目内容
已知函数f(x)是定义在R上的偶函数,且对任意的x∈R都有f(x+2)=f(x).当0≤x≤1时,f(x)=x2.若直线y=x+a与函数y=f(x)的图像在[0,2]内恰有两个不同的公共点,则实数a的值是( )
| A.0 | B.0或- | C.- 或- 或- | D.0或- |
D
解析试题分析:当0≤x≤1时,f(x)=x2. 又函数f(x)是定义在R上的偶函数,则当-1≤x≤0时,f(x)=x2; 对任意的x∈R都有f(x+2)=f(x),得f(x)周期为T=2.故当 时,
时, ,所以
,所以 ;函数y=f(x)在[0,2] 的图像,结合图形可知,直线y=x+a过原点时与函数y=f(x)有两交点,此时a="0;" 直线y=x+a与函数y=f(x),(0≤x≤1)的图像相切时恰有两交点,此时,
;函数y=f(x)在[0,2] 的图像,结合图形可知,直线y=x+a过原点时与函数y=f(x)有两交点,此时a="0;" 直线y=x+a与函数y=f(x),(0≤x≤1)的图像相切时恰有两交点,此时, ,得
,得 ,代入y=x+a得,
,代入y=x+a得, .
.
考点:函数的奇偶性、周期性、函数的零点.

练习册系列答案
相关题目
若函数 满足
满足 ,且
,且 时,
时, ,函数
,函数 ,则函数
,则函数 在区间
在区间 内的零点的个数为
内的零点的个数为
| A.6 | B.7 | C.8 | D.9 |
下列函数中,既是奇函数又是增函数的为( )
A.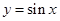 | B. | C. | D. |
有下列四个命题:
①对于 ,函数
,函数 满足
满足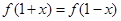 ,则函数
,则函数 的最小正周期为2;
的最小正周期为2;
②所有指数函数的图象都经过点 ;
;
③若实数 满足
满足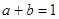 ,则
,则 的最小值为9;
的最小值为9;
④已知两个非零向量 ,
,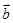 ,则“
,则“
 ”是“
”是“ ”的充要条件.
”的充要条件.
其中真命题的个数为( )
| A.0 | B.1 | C.2 | D.3 |
设 是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图像,则
是定义在R上的周期为3的周期函数,如图表示该函数在区间(-2,1]上的图像,则 +
+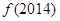 =( )
=( )
| A.3 | B.2 | C.1 | D.0 |
给定函数:① ;②
;② ;③
;③ ;④
;④ ,其中奇函数是( )
,其中奇函数是( )
| A.① | B.② | C.③ | D.④ |
 的图像大致是( )
的图像大致是( )
 ,若存在实数
,若存在实数 、
、 、
、 、
、 ,满足
,满足
 ,其中
,其中 ,则
,则 的取值范围是 .
的取值范围是 . 的反函数
的反函数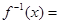 ________________.
________________.