题目内容
若函数
满足
，且
时，
，函数
，则函数
在区间
内的零点的个数为
| A．6 | B．7 | C．8 | D．9 |
C
解析试题分析：因为函数满足，所以函数是周期为2 的周期函数，又因为时，，所以作出函数的图像：
由图知：函数
－g(x)在区间内的零点的个数为8个.
考点：周期函数，函数零点.
练习册系列答案
相关题目
记实数
中的最大数为max{} , 最小数为min{}则max{min{
}}= （ ）
A． | B．1 | C．3 | D． |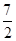
某流程图如图所示，现输入如下四个函数， 则可以输出的函数是 （ ）
A． | B． |
C． | D． |
已知函数
是
上的单调增函数且为奇函数，数列
是等差数列，
，则
的值（ ）
| A．恒为正数 | B．恒为负数 |
| C．恒为0 | D．可以为正数也可以为负数 |
的图象的交点个数为( ).已知函数
，若方程
有两个实数根，则
的取值范围是( )
A． | B． | C． | D． |
的图象如图所示，则导函数
的图象的大致形状是( )
已知函数f(x)是定义在R上的偶函数，且对任意的x∈R都有f(x＋2)＝f(x)．当0≤x≤1时，f(x)＝x2.若直线y＝x＋a与函数y＝f(x)的图像在[0,2]内恰有两个不同的公共点，则实数a的值是( )
| A．0 | B．0或－ | C．－ 或－ | D．0或－ |
函数
所有零点的和等于( )
| A．6 | B．7.5 | C．9 | D．12 |