题目内容
点P(1,1)平分椭圆
+
=1的一条弦,则这条弦所在直线的方程为
| x2 |
| 4 |
| y2 |
| 2 |
x+2y-2=0
x+2y-2=0
.分析:因为点P(1,1)在椭圆内,而且点P(1,1)是椭圆
+
=1的一条弦的中点,所以可用点差法求直线方程.具体过程是先设过点P的弦交椭圆与A(x1,y1),B(x2,y2),再将两点代入椭圆方程作差,由x1+x2=2,y1+y2=2即可得直线斜率,由点斜式写出所求方程即可
| x2 |
| 4 |
| y2 |
| 2 |
解答:解:设过点P的弦交椭圆与A(x1,y1),B(x2,y2)
则
+
=1,①
+
=1②
①-②,的,
+
=0
即
=-
∵x1+x2=2,y1+y2=2
∴
=-
=-
∴这条弦所在直线的斜率为-
弦所在直线的方程为y-1=-
(x-1)
即x+2y-2=0
故答案为x+2y-2=0
则
| x12 |
| 4 |
| y12 |
| 2 |
| x22 |
| 4 |
| y22 |
| 2 |
①-②,的,
| x12-x22 |
| 4 |
| y12-y22 |
| 2 |
即
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 2 |
∵x1+x2=2,y1+y2=2
∴
| y1-y2 |
| x1-x2 |
| x1+x2 |
| 2(y1+y2) |
| 1 |
| 2 |
∴这条弦所在直线的斜率为-
| 1 |
| 2 |
弦所在直线的方程为y-1=-
| 1 |
| 2 |
即x+2y-2=0
故答案为x+2y-2=0
点评:本题考查了直线与椭圆的关系,特别是当直线与椭圆相交,且已知中点坐标的情况下,用点差法可有效提高做题效率,做题时不妨用其它方法试试,比较不同解法之间的优劣.

练习册系列答案
相关题目
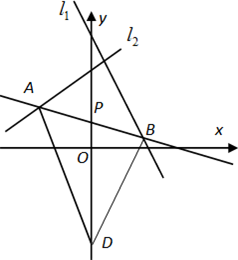 如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.
如图,直线L过点P(0,1),夹在两已知直线l1:2x+y-8=0和l2:x-3y+10=0之间的线段AB恰被点P平分.