题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,一条准线方程为
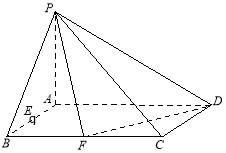
,一条准线方程为![]() 过椭圆的上顶点A作一条与x轴、y轴都不垂直的直线交椭圆于另一点P,P关于x轴的对称点为Q.
过椭圆的上顶点A作一条与x轴、y轴都不垂直的直线交椭圆于另一点P,P关于x轴的对称点为Q.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 若直线AP,AQ与x轴交点的横坐标分别为m,n,求证:mn为常数,并求出此常数.
若直线AP,AQ与x轴交点的横坐标分别为m,n,求证:mn为常数,并求出此常数.

【答案】(1)![]() ;(2)
;(2)![]() 为常数2.
为常数2.
【解析】
![]() 利用
利用![]() ,
,![]() ,及其
,及其![]() ,解出即可得出;
,解出即可得出;![]() 证法一:设P点坐标为
证法一:设P点坐标为![]() ,则Q点坐标为
,则Q点坐标为![]() 可得
可得![]() ,直线AP的方程为
,直线AP的方程为![]() 令
令![]() ,解得
,解得![]() 同理可得
同理可得![]() 再利用
再利用![]() 在椭圆
在椭圆![]() 上,即可得出mn;解法二:设直线AP的斜率为
上,即可得出mn;解法二:设直线AP的斜率为![]() ,则AP的方程为
,则AP的方程为![]() ,令
,令![]() ,得
,得![]() 联立
联立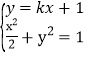 ,解得P,则可得Q点的坐标
,解得P,则可得Q点的坐标![]() 可得
可得![]() ,可得直线AQ的方程,可得n,即可得出.
,可得直线AQ的方程,可得n,即可得出.
![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
![]() .
.
故椭圆的方程为![]() .
.
![]() 证法一:设P点坐标为
证法一:设P点坐标为![]() ,则Q点坐标为
,则Q点坐标为![]()
![]() ,
,
![]() 直线AP的方程为
直线AP的方程为![]() .
.
令![]() ,解得
,解得![]() .
.
![]() ,
,
![]() 直线AQ的方程为
直线AQ的方程为![]() .
.
令![]() ,解得
,解得![]() .
.
![]() .
.
又![]() 在椭圆
在椭圆![]() 上,
上,
![]() ,即
,即![]() ,
,
![]() .
.
![]() 以mn为常数,且常数为2.
以mn为常数,且常数为2.
解法二:设直线AP的斜率为![]() ,则AP的方程为
,则AP的方程为![]() ,
,
令![]() ,得
,得![]() .
.
联立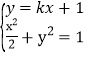
消去y,得![]() ,解得
,解得![]() ,
,![]() ,
,
![]() ,
,
则Q点的坐标为![]()
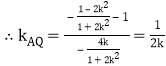 ,
,
故直线AQ的方程为![]() .
.
令![]() ,得
,得![]() ,
,
![]() .
.
![]() 为常数,常数为2.
为常数,常数为2.

练习册系列答案
相关题目
【题目】某中学高一女生共有450人,为了了解高一女生的身高情况,随机抽取部分高一女生测量身高,所得数据整理后列出频率分布表如下:
组别 | 频数 | 频率 |
145.5~149.5 | 8 | 0.16 |
149.5~153.5 | 6 | 0.12 |
153.5~157.5 | 14 | 0.28 |
157.5~161.5 | 10 | 0.20 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 |
|
|
合计 |
|
|
(1)求出表中字母![]() 所对应的数值;
所对应的数值;
(2)在给出的直角坐标系中画出频率分布直方图;
(3)估计该校高一女生身高在149.5~165.5![]() 范围内有多少人?
范围内有多少人?