题目内容
在区间 内任取一个实数x,则所取实数x落在函数
内任取一个实数x,则所取实数x落在函数 增区间内的概率为 .
增区间内的概率为 .
【答案】分析:根据几何概型公式,将符合题意的落在函数 增区间内的区间长度除以总的区间长度,即得本题的概率.
增区间内的区间长度除以总的区间长度,即得本题的概率.
解答:解:由函数 的解析式得,
的解析式得,
增区间满足 2kπ- ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,
,
∴2kπ- ≤2x≤2kπ+
≤2x≤2kπ+ ,
,
⇒kπ- ≤x≤kπ+
≤x≤kπ+ ,k∈Z,又x∈
,k∈Z,又x∈ ,
,
∴- ≤x≤
≤x≤ ,其长度为
,其长度为 ,
,
记事件A=“实数x落在函数 增区间内”,
增区间内”,
∵区间 长度是π,
长度是π,
∴由几何概型公式,得P(A)= =
= .
.
故答案为: .
.
点评:本题主要考查了几何概型和概率的意义等知识,解题的关键是利用几何概型公式,属于基础题.
 增区间内的区间长度除以总的区间长度,即得本题的概率.
增区间内的区间长度除以总的区间长度,即得本题的概率.解答:解:由函数
 的解析式得,
的解析式得,增区间满足 2kπ-
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,
,∴2kπ-
 ≤2x≤2kπ+
≤2x≤2kπ+ ,
,⇒kπ-
 ≤x≤kπ+
≤x≤kπ+ ,k∈Z,又x∈
,k∈Z,又x∈ ,
,∴-
 ≤x≤
≤x≤ ,其长度为
,其长度为 ,
,记事件A=“实数x落在函数
 增区间内”,
增区间内”,∵区间
 长度是π,
长度是π,∴由几何概型公式,得P(A)=
 =
= .
.故答案为:
 .
.点评:本题主要考查了几何概型和概率的意义等知识,解题的关键是利用几何概型公式,属于基础题.

练习册系列答案
相关题目
分别在区间[1,6]和[1,4]内任取一个实数,依次记为m和n,则m>n的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分别在区间[0,1]和[0,2]内任取一个实数,依次记为m和n,则m2<n的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 内任取一个实数x,则所取实数x落在函数
内任取一个实数x,则所取实数x落在函数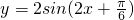 增区间内的概率为________.
增区间内的概率为________.