题目内容
11.若点A($\sqrt{2}$,2)在幂函数f(x)的图象上,点B(-2,$\frac{1}{4}$)在幂函数g(x)的图象上,定义h(x)=$\left\{\begin{array}{l}{f(x)}&{f(x)≤g(x)}\\{g(x)}&{f(x)>g(x)}\end{array}\right.$.(1)试求函数h(x)的最小值以及单调区间;
(2)若方程h(x)-k=0在R上有四解,求k的取值范围.
分析 (1)求出分段函数的解析式,然后求解函数的最值以及函数的单调区间.
(2)画出函数的图象,利用方程的四个解,推出k的范围.
解答 解:(1)设f(x)=xα,点A($\sqrt{2}$,2)在幂函数f(x)的图象上,
可得2=$(\sqrt{2})^{α}$,α=2,f(x)=x2.
设g(x)=xα,点B(-2,$\frac{1}{4}$)在幂函数g(x)的图象上,
可得$\frac{1}{4}={(-2)}^{α}$,解得α=-2,
g(x)=x-2.
h(x)=$\left\{\begin{array}{l}{f(x)}&{f(x)≤g(x)}\\{g(x)}&{f(x)>g(x)}\end{array}\right.$.
可得h(x)=$\left\{\begin{array}{l}{x}^{2},x∈(-∞,-1]∪[1,+∞)\\{x}^{-2},x∈(-1,0)∪(0,1)\end{array}\right.$.函数的图象如图: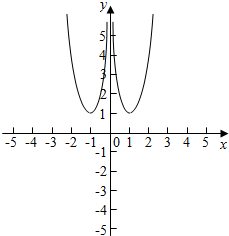
函数的最小值为1,单调减区间为:(-∞,-1),(0,1);单调增区间(-1,0),(1,+∞).
(2)方程h(x)-k=0在R上有四解,
可知y=h(x)与y=k有四个交点.由函数的图象可知k>1.
点评 本题考查函数的图象,幂函数的解析式的求法,函数的零点的个数,考查计算能力.

练习册系列答案
相关题目
6.等比数列{an}中,a2=2,a5=$\frac{1}{4}$,则公比q=( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
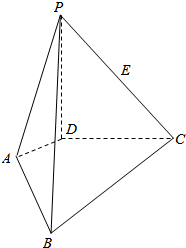 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.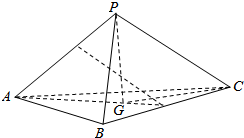 三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=点2$\sqrt{11}$,P在平面ABC内的射影恰为△ABC的重心G(即△ABC三条中线的交点).
三棱锥P-ABC中,AB=AC=2$\sqrt{10}$,BC=4,PC=点2$\sqrt{11}$,P在平面ABC内的射影恰为△ABC的重心G(即△ABC三条中线的交点). 如图,在斜三棱柱ABC-A1B1C1中,D是BC的中点,求证:A1C∥平面AB1D.
如图,在斜三棱柱ABC-A1B1C1中,D是BC的中点,求证:A1C∥平面AB1D.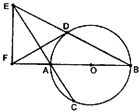 如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图,AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.