题目内容
1.已知函数f(x)=lnx,g(x)=$\frac{t}{x}$-lnx.(1)如果函数g(x)≤f(x)恒成立,求t的取值范围;
(2)设函数F(x)=f(x)-$\frac{1}{{e}^{x}}$+$\frac{2}{ex}$.试问函数F(x)是否存在零点,若存在,求出零点个数,若不存在,请说明理由.
分析 (1)把恒成立问题转换为求2xlnx的最小值问题,利用导数求出最小值
(2)把函数整理成F(x)=lnx-$\frac{1}{{e}^{x}}$+$\frac{2}{ex}$≥$-\frac{1}{ex}$-$\frac{1}{{e}^{x}}$+$\frac{2}{ex}$=$\frac{1}{x}$($\frac{1}{e}$-$\frac{x}{{e}^{x}}$),要判断是否有零点,只需看F(x)的正负问题,令G(x)=$\frac{1}{e}$-$\frac{x}{{e}^{x}}$,利用导数分析G(x)
解答 解:(1)∵$\frac{t}{x}$-lnx≤lnx恒成立,
∴t≤2xlnx恒成立.
令h(x)=2xlnx,
h'(x)=2(1+lnx),
当x∈(0,$\frac{1}{e}$)时,h'(x)<0,h(x)递减;
当x∈($\frac{1}{e}$,+∞)时,h'(x)>0,h(x)递增;
∴h(x)的最小值为h($\frac{1}{e}$)=-$\frac{2}{e}$,
∴t≤-$\frac{2}{e}$.
(2)由(1)知,2xlnx≥-$\frac{2}{e}$,
∴lnx≥$-\frac{1}{ex}$,
F(x)=f(x)-$\frac{1}{{e}^{x}}$+$\frac{2}{ex}$ ①
∴F(x)=lnx-$\frac{1}{{e}^{x}}$+$\frac{2}{ex}$≥$-\frac{1}{ex}$-$\frac{1}{{e}^{x}}$+$\frac{2}{ex}$=$\frac{1}{x}$($\frac{1}{e}$-$\frac{x}{{e}^{x}}$),
令G(x)=$\frac{1}{e}$-$\frac{x}{{e}^{x}}$则g'(x)=$\frac{x-1}{{e}^{x}}$,
当x∈(0,1)时,G'(x)<0,G(x)递减;
当x∈(1,+∞)时,G'(x)>0,G(x)递增;
∴G(x)≥G(1)=0 ②
∴F(x)=lnx-$\frac{1}{{e}^{x}}$+$\frac{2}{ex}$≥$-\frac{1}{ex}$-$\frac{1}{{e}^{x}}$+$\frac{2}{ex}$=$\frac{1}{x}$($\frac{1}{e}$-$\frac{x}{{e}^{x}}$)≥0,
∵①②中取等号的条件不同,
∴F(x)>0,
故函数没有零点.
点评 考查了恒成立问题和利用导函数研究原函数的最值问题.

 阅读快车系列答案
阅读快车系列答案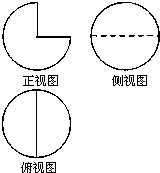
| A. | 8π | B. | 16π | C. | $\frac{8π}{3}$ | D. | $\frac{16π}{3}$ |
| A. | 4$\sqrt{3}$ | B. | $\frac{24\sqrt{13}}{13}$ | C. | $\frac{12\sqrt{13}}{13}$ | D. | 8$\sqrt{3}$ |
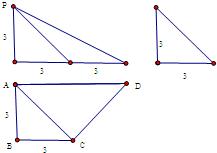 已知四棱锥P-ABCD的三视图如图所示,
已知四棱锥P-ABCD的三视图如图所示,
 已知:正方体ABCD-A1B1C1D1,边长为1,E为棱CC1的中点.
已知:正方体ABCD-A1B1C1D1,边长为1,E为棱CC1的中点.