题目内容
【题目】如图在△ABC中,已知点D在BC边上,满足AD⊥AC,cos ∠BAC=-![]() ,AB=3
,AB=3![]() ,BD=
,BD=![]() .
.
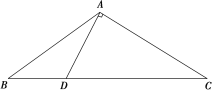
(1)求AD的长;
(2)求△ABC的面积.
【答案】见解析
【解析】(1)因为AD⊥AC,cos ∠BAC=-![]() ,
,
所以sin ∠BAC=![]() .
.
又sin ∠BAC=sin![]() =cos ∠BAD=
=cos ∠BAD=![]() ,
,
在△ABD中,BD2=AB2+AD2-2AB·AD·cos ∠BAD,
即AD2-8AD+15=0,
解得AD=5或AD=3,由于AB>AD,
所以AD=3.
(2)在△ABD中,![]() =
=![]() ,
,
又由cos ∠BAD=![]() 得sin ∠BAD=
得sin ∠BAD=![]() ,所以sin ∠ADB=
,所以sin ∠ADB=![]() ,则sin ∠ADC=sin(π-∠ADB)=sin ∠ADB=
,则sin ∠ADC=sin(π-∠ADB)=sin ∠ADB=![]() .
.
因为∠ADB=∠DAC+∠C=![]() +∠C,所以cos ∠C=
+∠C,所以cos ∠C=![]() .
.
在Rt△ADC中,cos ∠C=![]() ,则tan ∠C=
,则tan ∠C=![]() =
=![]() =
=![]() ,
,
所以AC=3![]() ,
,
则△ABC的面积S=![]() AB·AC·sin ∠BAC=
AB·AC·sin ∠BAC=![]() ×3
×3![]() ×3
×3![]() ×
×![]() =6
=6![]() .
.

练习册系列答案
相关题目
