题目内容

方程x2+(m-1)x+m2-2=0的两个根一个小于-1，另一个大于1，那么实数m的取值范围是（    ）

A.(-,)          B.(-2,0)            C.(-2,1)          D.(0,1)

解析:设f(x)=x2+(m-1)x+m2-2,

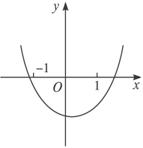
由条件可知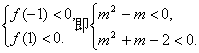

∴0＜m＜1.

答案:D


练习册系列答案
相关题目
已知方程
x2
|m|-1
+
y2
2-m
=1表示焦点在y轴上的椭圆，则m的取值范围是（　　）
A、m＜2
B、1＜m＜2
C、m＜-1或1＜m＜2
D、m＜-1或1＜m＜
3
2
如果方程
x2
|m|-1
+
y2
2-m
=1表示双曲线，则实数m的取值范围为
 
．
方程
x2
|m|-1
+
y2
2
=1表示焦点在y轴上的椭圆时，实数m的取值范围是
（-3，-1）∪（1，3）
（-3，-1）∪（1，3）
．
已知方程
x2
|m|-1
+
y2
2-m
=1表示焦点在y轴上的椭圆，则m的取值范围是
{m|1＜m＜
3
2
或m＜-1}
{m|1＜m＜
3
2
或m＜-1}
．
如果方程
x2
|m|-1
-
y2
m-2
=1表示双曲线，那么实数m的取值范围是（　　）
A、m＞2
B、m＜1或m＞2
C、-1＜m＜2
D、-1＜m＜1或m＞2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网