题目内容
已知公比大于1的等比数列{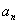 }满足:
}满足: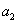 +
+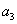 +
+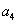 =28,且
=28,且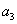 +2是
+2是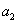 和
和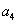 的等差中项.(Ⅰ)求数列{
的等差中项.(Ⅰ)求数列{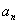 }的通项公式;
}的通项公式;
(Ⅱ)若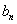 =
=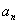
 ,求{
,求{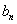 }的前n项和
}的前n项和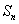 .
.
(Ⅰ)q=2, =2,{
=2,{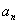 }的通项公式
}的通项公式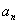 =
= ;
;
(Ⅱ)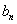 =-n
=-n ,
, 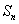 =(1-n)
=(1-n) -2
-2
解析试题分析:解:由已知得
解得: (舍)
(舍)
∴
故可知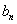 =-n
=-n ,
, 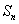 =(1-n)
=(1-n) -2
-2
那么结合错位相减法来得到数列的求和,那么可知为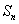 =(1-n)
=(1-n) -2
-2
考点:等比数列和等差数列的求和公式
点评:本题考查等比数列的通项公式和求和公式,属基础题

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
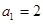 ,点
,点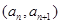 在函数
在函数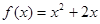 的图像上,(其中
的图像上,(其中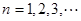 )
)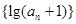 是等比数列;
是等比数列;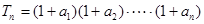 ,求
,求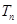 及数列
及数列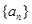 的通项.
的通项.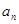 }的前n 项和为
}的前n 项和为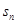 ,已知
,已知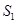 ,
,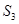 ,
,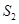 成等差数列。
成等差数列。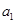 -
-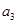 =3,求
=3,求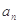 }的公比为q,前n项和为Sn,且S1,S3,S2成等差数列.
}的公比为q,前n项和为Sn,且S1,S3,S2成等差数列.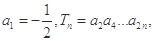 ,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由。
,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由。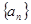 是各项为正数的等比数列,且a1=1,a2+a3=6,
是各项为正数的等比数列,且a1=1,a2+a3=6,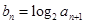 ,
,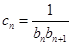 求该数列
求该数列 的前n项和
的前n项和
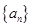 中,
中,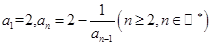
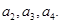 (2)试猜想
(2)试猜想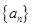 中,
中,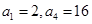 ,
,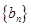 中,
中,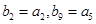 ,求数列
,求数列 项和
项和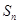 。
。 中,前n项和为
中,前n项和为 ,且
,且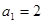 ,且
,且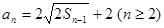 .
.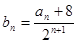 ,
,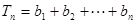 ,证明
,证明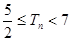 .
.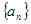 的前
的前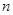 项和为
项和为 ,
,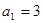 ,若数列
,若数列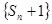 是公比为
是公比为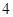 的等比数列.
的等比数列. 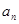 ;
;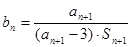 ,
,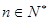 ,求数列
,求数列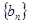 的前
的前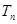 .
.