题目内容
正项数列 中,前n项和为
中,前n项和为 ,且
,且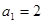 ,且
,且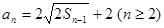 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设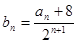 ,
,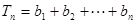 ,证明
,证明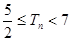 .
.
(1)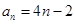 (2)
(2) ,利用错位相减法求得前n项和,依据和中
,利用错位相减法求得前n项和,依据和中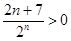 可知
可知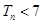 ,再结合数列是递增的可知
,再结合数列是递增的可知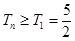
解析试题分析:(1) 由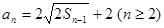 得
得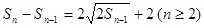
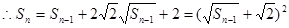 ,
,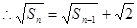
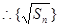 是首项为
是首项为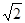 公差为
公差为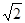 的等差数列,
的等差数列,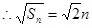 ,
, ,
, ,对n=1也成立,
,对n=1也成立,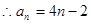
(2) ,
,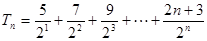
 ,两式相减,得
,两式相减,得

下面证明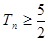 ,
, 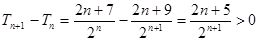 ,
,
或

 ,
,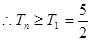 ,
,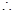
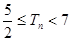
考点:数列求通项求和
点评:本题中求通项主要是由前n项和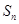 求
求 ,
, ,由已知条件先求得
,由已知条件先求得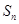 在求
在求 较简单,求和时应用的错位相减法,这种方法适用于通项公式为n的一次式与指数式乘积的形式
较简单,求和时应用的错位相减法,这种方法适用于通项公式为n的一次式与指数式乘积的形式

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
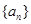 的前三项和为18,
的前三项和为18,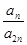 是一个与
是一个与 无关的常数,若
无关的常数,若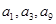 恰为等比数列
恰为等比数列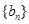 的前三项,
的前三项,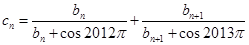 ,
,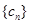 的前三
的前三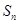 ,求证:
,求证: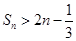
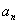 }满足:
}满足: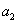 +
+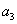 +
+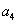 =28,且
=28,且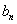 =
= ,求{
,求{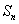 .
.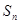 是等比数列
是等比数列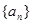 的前
的前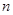 项和, 公比
项和, 公比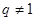 ,已知1是
,已知1是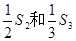 的等 差中项,6是
的等 差中项,6是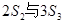 的等比中项,
的等比中项, 中,
中, ,求其第4项及前5项和.
,求其第4项及前5项和. 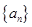 的各项均为正数,且
的各项均为正数,且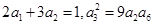
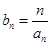 ,求数列
,求数列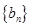 的前n项和
的前n项和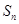 .
.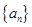 的各项均为正数,且
的各项均为正数,且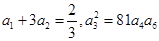
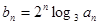 求数列
求数列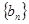 的前
的前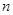 项和
项和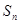 .
.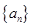 的前
的前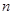 项和为
项和为 ,满足
,满足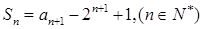 ,且
,且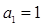 。
。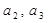 的值;
的值;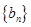 的前
的前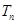 ,且
,且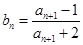 ,证明:对一切正整数
,证明:对一切正整数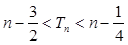
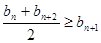 ;②
;②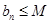 (
(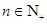 ,
,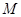 是与
是与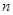 无关的常数)的无穷数列
无关的常数)的无穷数列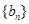 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列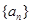 的前
的前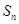 满足:
满足: 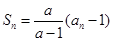 (
(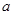 为常数,且
为常数,且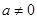 ,
,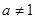 ).
). 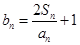 ,若数列
,若数列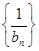 为“嘉文”数列.
为“嘉文”数列.