题目内容
等比数列{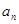
}的前n 项和为
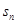，已知
,
,
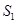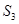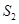成等差数列。
（1）求{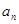}的公比q； （2）求
－
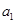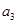＝3，求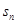
（1）
（2）
解析试题分析：解：（Ⅰ）依题意有 
由于 
，故
又
，从而
（Ⅱ）由已知可得
故
，结合等差数列的前n项和公式可知，
从而
考点：等差数列
点评：主要是考查了等差数列的通项公式和求和的运用，属于中档题。
练习册系列答案
相关题目
题目内容
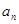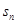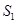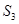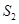等比数列{}的前n 项和为，已知,,成等差数列。
（1）求{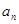}的公比q； （2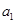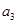）求－＝3，求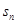
（1）
（2）
解析试题分析：解：（Ⅰ）依题意有
由于 ，故
又，从而
（Ⅱ）由已知可得
故，结合等差数列的前n项和公式可知，
从而
考点：等差数列
点评：主要是考查了等差数列的通项公式和求和的运用，属于中档题。
满足：
，且
是
、
的等差中项.
，求数列
的前
项和
.
的前三项和为18，
是一个与
无关的常数，若
恰为等比数列
的前三项，
，
的前三
，求证：
中，
是数列
的前
项和，对任意
，有
.函数
，数列
的首项
求证：
是等比数列并求
，
，求数列
的前n项和
.
、
满足：
.
；
为等差数列，并求数列
，求实数
为何值时
恒成立。
为等比数列，且
，
，该数列的各项都为正数，求
；（2）若等比数列
，末项
，公比
，求项数
。
}满足：
+
+
=28，且
=
，求{
.
的各项均为正数，且
求数列
的前
项和
.