题目内容
(本题满分14分)已知数列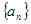 的前
的前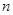 项和为
项和为 ,
,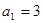 ,若数列
,若数列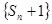 是公比为
是公比为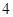 的等比数列.
的等比数列.
(Ⅰ)求数列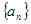 的通项公式
的通项公式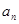 ;
;
(Ⅱ)设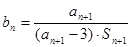 ,
,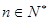 ,求数列
,求数列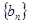 的前
的前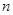 项和
项和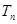 .
.
(Ⅰ) ;(Ⅱ)
;(Ⅱ)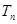
 。
。
解析试题分析:(Ⅰ) ,
,  ,
,
当 时,
时, ,且
,且 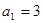 ,
, ,
,
所以数列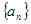 的通项公式为
的通项公式为 .…………………………7分
.…………………………7分
(Ⅱ)

 .……………14分
.……………14分
考点:等比数列的性质;数列通项公式的求法;数列前n项和的求法。
点评:我们要熟练掌握求数列通项公式的方法。公式法是求数列通项公式的基本方法之一,常用的公式有:等差数列的通项公式、等比数列的通项公式及公式 。此题的第一问求数列的通项公式就是用公式
。此题的第一问求数列的通项公式就是用公式 ,用此公式要注意讨论
,用此公式要注意讨论 的情况。
的情况。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
数列 的前
的前 项和为
项和为 ,若
,若 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
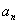 }满足:
}满足: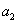 +
+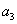 +
+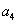 =28,且
=28,且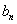 =
= ,求{
,求{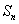 .
.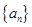 的各项均为正数,且
的各项均为正数,且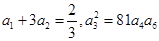
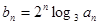 求数列
求数列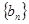 的前
的前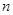 项和
项和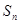 .
.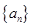 的前
的前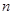 项和为
项和为 ,满足
,满足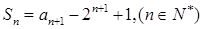 ,且
,且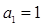 。
。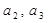 的值;
的值;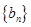 的前
的前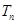 ,且
,且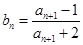 ,证明:对一切正整数
,证明:对一切正整数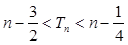
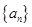 的前
的前 项和为
项和为 ,
, ,
, ,求数列
,求数列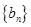
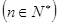 是递增的等比数列,且
是递增的等比数列,且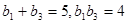 .
.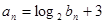 ,求证数列
,求证数列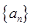 是等差数列;
是等差数列;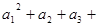 ……
……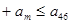 ,求
,求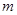 的最大值.
的最大值.  1.921,1.07510
1.921,1.07510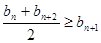 ;②
;②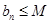 (
(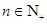 ,
,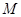 是与
是与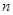 无关的常数)的无穷数列
无关的常数)的无穷数列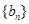 叫“嘉文”数列.已知数列
叫“嘉文”数列.已知数列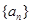 的前
的前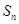 满足:
满足: 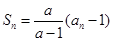 (
(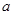 为常数,且
为常数,且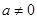 ,
,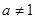 ).
). 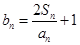 ,若数列
,若数列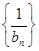 为“嘉文”数列.
为“嘉文”数列.