题目内容
关于函数f(x)=4sin  (x∈R),有下列命题:
(x∈R),有下列命题:
①由f(x1)=f(x2)=0可得x1-x2必是π的整数倍;
②y=f(x)的表达式可改写为y=4cos  ;
;
③y=f(x)的图象关于点 对称;
对称;
④y=f(x)的图象关于直线x=- 对称.
对称.
其中正确命题的序号是________(把你认为正确的命题序号都填上).
②③
解析 函数f(x)=4sin 的最小正周期T=π,由相邻两个零点的横坐标间的距离是
的最小正周期T=π,由相邻两个零点的横坐标间的距离是 =
= 知①错.
知①错.
利用诱导公式得f(x)=4cos =
=
4cos =4cos
=4cos ,知②正确.
,知②正确.
由于曲线f(x)与x轴的每个交点都是它的对称中心,将x=- 代入得f(x)=4sin
代入得f(x)=4sin =4sin 0=0,
=4sin 0=0,
因此点 是f(x)图象的一个对称中心,故命题③正确.曲线f(x)的对称轴必经过图象的最高点或最低点,且与y轴平行,而x=-
是f(x)图象的一个对称中心,故命题③正确.曲线f(x)的对称轴必经过图象的最高点或最低点,且与y轴平行,而x=- 时y=0,点
时y=0,点 不是最高点也不是最低点,故直线x=-
不是最高点也不是最低点,故直线x=- 不是图象的对称轴,因此命题④不正确.
不是图象的对称轴,因此命题④不正确.

练习册系列答案
相关题目
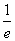 C.
C.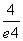 D.
D.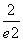
 (k∈Z).
(k∈Z).

 +2a+b,当x∈
+2a+b,当x∈ 时,-5≤f(x)≤1.
时,-5≤f(x)≤1. 且lg g(x)>0,求g(x)的单调区间.
且lg g(x)>0,求g(x)的单调区间. 个单位长度后,所得的图象与原图象重合,则ω的最小值等于( ).
个单位长度后,所得的图象与原图象重合,则ω的最小值等于( ). B.3 C.6 D.9
B.3 C.6 D.9 =
= ,α∈
,α∈ ,则cos α=________.
,则cos α=________. b|,则下面结论正确的是( )
b|,则下面结论正确的是( )