题目内容
已知关于x的方程lnx-ax=0恰有一个实根,则实数a的取值范围______.
设y=lnx-ax,则y'=
-a=0,x=
,y“=-
<0
当a≤0,y'>0,最多有一个实根,因 y(0-)<0,y(1)≥0,所以(0,1]之间必有一个实根
a>0,x=
,y=-lna-1为极大值,此极大值若为0的话,则有一个实根,此时a=
此极大值若大于0的话,会有两个实根,此极大值若小于0的话,则无实根.
因此a的取值范围为:(-∞,0]∪{
},
故答案为(-∞,0]∪{
}
| 1 |
| x |
| 1 |
| a |
| 1 |
| x2 |
当a≤0,y'>0,最多有一个实根,因 y(0-)<0,y(1)≥0,所以(0,1]之间必有一个实根
a>0,x=
| 1 |
| a |
| 1 |
| e |
因此a的取值范围为:(-∞,0]∪{
| 1 |
| e |
故答案为(-∞,0]∪{
| 1 |
| e |

练习册系列答案
相关题目
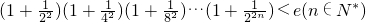 .
. .
.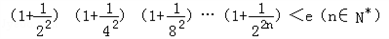 .
.