题目内容
过原点且与双曲线
只有一个公共点的直线的条数是（ ）A．3
B．2
C．1
D．0
【答案】分析：设过原点的直线方程为y=kx，联立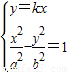
，得（b2-a2k2）x2-a2b2=0，由过原点的直线与双曲线
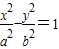只有一个公共点，得k=
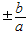．由y=
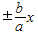是双曲线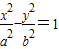
的渐近线，能求出结果．
解答：解：设过原点的直线方程为y=kx，
联立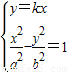
，得（b2-a2k2）x2-a2b2=0，
∵过原点的直线与双曲线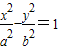
只有一个公共点，
∴△=4（b2-a2k2）a2b2=0，
解得k=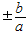
．
∵y=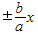
是双曲线
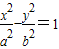的渐近线，
∴过原点且与双曲线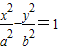
只有一个公共点的直线的条数是0条．
故选D．
点评：本题考查直线与双曲线的位置关系，解题时要认真审题，仔细解答，注意合理地进行等价转化．
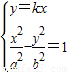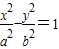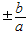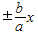，得（b2-a2k2）x2-a2b2=0，由过原点的直线与双曲线只有一个公共点，得k=．由y=是双曲线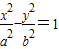的渐近线，能求出结果．解答：解：设过原点的直线方程为y=kx，
联立
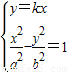，得（b2-a2k2）x2-a2b2=0，∵过原点的直线与双曲线
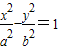只有一个公共点，∴△=4（b2-a2k2）a2b2=0，
解得k=
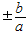．∵y=
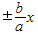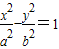是双曲线的渐近线，∴过原点且与双曲线
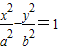只有一个公共点的直线的条数是0条．故选D．
点评：本题考查直线与双曲线的位置关系，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
，0）为圆心，1为半径的圆相切，双曲线S的一个顶点A′与A关于直线y=x对称，设直线l过点A，且斜率为k. 
；
，求斜率k的值及相应的点B的坐标.
只有一个公共点的直线的条数是（ ）