题目内容
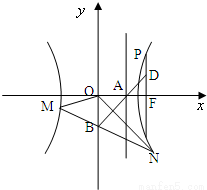
如图,已知双曲线S的两条渐近线过坐标原点且与以点A(
(1)求双曲线S的方程;
(2)当k=1时,在双曲线S的上支上求点B,使其与直线l的距离为![]() ;
;
(3)当0≤k<1时,若双曲线S的上支上有且只有一个点B到直线l的距离为![]() ,求斜率k的值及相应的点B的坐标.
,求斜率k的值及相应的点B的坐标.
思路解析:本题是直线方程、点到直线的距离、圆、双曲线等知识的综合运用.(1)、(2)按条件求解不难.(3)可用数形结合,作一条与l平行且与l相距为![]() 的直线l′,使l′与双曲线S的上支相切,切点即为所求.
的直线l′,使l′与双曲线S的上支相切,切点即为所求.
解:(1)由已知得双曲线的渐近线为y=±x,因而S为等轴双曲线,顶点A′与A(![]() ,0)关于直线y=x对称.∴A′(0,
,0)关于直线y=x对称.∴A′(0,![]() ),∴所求双曲线S的方程为y2-x2=2.
),∴所求双曲线S的方程为y2-x2=2.
(2)若B(x,![]() )是双曲线S的上支上到l:y=x-
)是双曲线S的上支上到l:y=x-![]() 的距离为
的距离为![]() 的点,则
的点,则![]() =
=![]() ,解得x=
,解得x=![]() ,y=2,∴点B的坐标为(
,y=2,∴点B的坐标为(![]() ,2).
,2).
(3)当0≤k<1时,双曲线S的上支在直线l的上方,∴点B在直线l的上方,设直线l′与l:y=k(x-![]() )平行且距离为
)平行且距离为![]() ,直线l′在l的上方,双曲线S的上支上有且只有一个点B到直线l的距离为
,直线l′在l的上方,双曲线S的上支上有且只有一个点B到直线l的距离为![]() ,等价于直线l′与双曲线S的上支有且只有一个公共点.设l′的方程为y=kx+m,由于l上的点A到l′的距离为
,等价于直线l′与双曲线S的上支有且只有一个公共点.设l′的方程为y=kx+m,由于l上的点A到l′的距离为![]() ,可知
,可知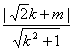 =
=![]() ,解得m=
,解得m=![]() (±
(±![]() -k).∵直线l′在直线l的上方,∴m=
-k).∵直线l′在直线l的上方,∴m=![]() (
(![]() -k).由方程y2-x2=2及y=kx+m消去y,得(k2-1)x2+2mkx+m2-2=0.
-k).由方程y2-x2=2及y=kx+m消去y,得(k2-1)x2+2mkx+m2-2=0.
∵k2≠1,∴Δ=4(m2-2+2k2)=8k(3k-2![]() ).
).
令Δ=0,∵0≤k<1,解得k=0或k=![]()
![]() .
.
当k=0时,m=![]() ,解得点B的坐标为(0,
,解得点B的坐标为(0, ![]() );
);
当k=![]()
![]() 时,m=
时,m=![]() ,解得点B的坐标为(2
,解得点B的坐标为(2![]() ,
,![]() ).
).

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
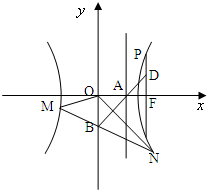 (2008•湖北模拟)如图,已知双曲线
(2008•湖北模拟)如图,已知双曲线
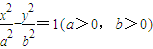 ,其右准线交x轴于点A,双曲线虚轴的下端点为B.过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足
,其右准线交x轴于点A,双曲线虚轴的下端点为B.过双曲线的右焦点F(c,0)作垂直于x轴的直线交双曲线于点P,若点D满足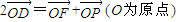 ,
,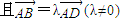 .
.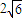 ,求l的方程.
,求l的方程.