题目内容
9.已知向量$\overrightarrow m$=(1,-2),$\overrightarrow n$=(1,1),且向量$\overrightarrow m$与$\overrightarrow m$+λ$\overrightarrow n$垂直,则λ=( )| A. | $\frac{5}{3}$ | B. | -$\frac{5}{3}$ | C. | 5 | D. | -5 |
分析 利用两个向量垂直等价于其的数量积等于0,解出λ值.
解答 解:∵$\overrightarrow m$=(1,-2),$\overrightarrow n$=(1,1),
∴$\overrightarrow{m}•\overrightarrow{n}$=1×1-2×1=-1,|$\overrightarrow m$|=$\sqrt{{1}^{2}+(-2)^{2}}$=$\sqrt{5}$
∵$\overrightarrow m$与$\overrightarrow m$+λ$\overrightarrow n$垂直,
∴$\overrightarrow m$•($\overrightarrow m$+λ$\overrightarrow n$)=|$\overrightarrow m$|2+λ$\overrightarrow{m}•\overrightarrow{n}$=5-λ=0,
解得λ=5,
故选:C.
点评 本题考查两个向量的数量积公式的应用,两个向量垂直的性质.

练习册系列答案
相关题目
17.若集合A={x|-1≤x≤1},B={x|0<x≤2},则A∩B=( )
| A. | {x|0<x≤1} | B. | {x|-1≤x<0} | C. | {x|0≤x≤2} | D. | {x|0≤x≤1} |
4.sin(-$\frac{2}{3}$π)=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
19.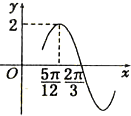 已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
 已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )| A. | [-$\frac{π}{12}$,$\frac{5π}{12}$] | B. | [-$\frac{7π}{12}$,-$\frac{1}{12}$π] | C. | [-$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [-$\frac{7π}{12}$,$\frac{5π}{12}$] |