题目内容
7.设f(x)=$\frac{x+1}{x}+a1nx(x>0)$.(1)求f(x)的单调区间;
(2)证明:0≤a≤1时,函数f(x)在(0,+∞)上没有零点;
(3)设F(x)=f(x)-$\frac{1}{x}$(a>0,x>0).A(x1y1)B(x2,y2)、C(x3,y3)依次是函数F(x)的图象上从左至右的三点. 证明:△ABC是钝角三角形.
分析 (1)求导数,分类讨论,即可求f(x)的单调区间;
(2)分类讨论,证明f(x)>0,即可证明:0≤a≤1时,函数f(x)在(0,+∞)上没有零点;
(3)先表示出向量BA、向量BC,根据向量的数量积运算求出角B的余弦值小于0得到B为钝角,从而得证.
解答 (1)解:由题意,f′(x)=$\frac{ax-1}{{x}^{2}}$.
①a≤0,f′(x)<0,f(x)在(0,+∞)上单调递减;
②a>0,x∈(0,$\frac{1}{a}$),f′(x)<0,函数单调递减,x∈($\frac{1}{a}$,+∞),f′(x)>0,函数单调递增;
(2)证明:由(1)可知,a=0时,f(x)=1+$\frac{1}{x}$>0恒成立,函数在(0,+∞)上没有零点;
a∈(0,1),x>0,f(x)min=f($\frac{1}{a}$)=1+a+aln$\frac{1}{a}$>0,
综上所述,0≤a≤1时,函数f(x)在(0,+∞)上没有零点;
(3)解:F′(x)=$\frac{a}{x}$>0,函数在(0,+∞)上单调递增.
由x1<x2<x3,
由(1)知y1<y2<y3,
∵$\overrightarrow{BA}$=(x1-x2,y1-y2),$\overrightarrow{BC}$=(x3-x2,y3-y2),
∴$\overrightarrow{BA}$•$\overrightarrow{BC}$=(x1-x2)(x3-x2)+(y1-y2)(y3-y2)<0,
∴∠ABC为钝角,即△ABC是钝角三角形.
点评 本题主要考查函数单调性与其导函数的正负之间的关系,以及向量的数量积运算.属中档题.

练习册系列答案
相关题目
15.若${(a+i)^2}-\frac{1}{i}∈R(a∈R,i$是虚数单位),则a=( )
| A. | 1 | B. | 0 | C. | 一$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
12.在△ABC中,tanC=2,BC边上的高为AD,D为垂足,且BD=2DC,则cosA=( )
| A. | $\frac{3}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$ |
9.已知集合A={0,1,2},B={1,m},若A∩B=B,则实数m的取值集合是( )
| A. | {0} | B. | {2} | C. | {0,2} | D. | {0,1,2} |
10.已知向量$\overrightarrow{AB}$、$\overrightarrow{AC}$、$\overrightarrow{AD}$满足$\overrightarrow{AC}$=$\overrightarrow{AB}$+$\overrightarrow{AD}$,|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,E、F分别是线段BC、CD的中点,若$\overrightarrow{DE}$•$\overrightarrow{BF}$=-$\frac{5}{4}$,则向量$\overrightarrow{AB}$与$\overrightarrow{AD}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
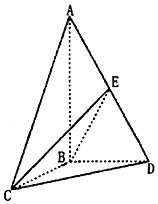 如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.
如图,三棱锥A-BCD中,AB⊥平面BCD,AC=AD=2,BC=BD=1,点E是线段AD的中点.