Question

【题目】在如图所示的多面体中， 平面 是的中点．

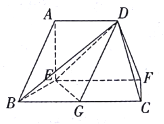
（1）求证： ；

（2）求二面角的余弦值．

Answer 1

【答案】(1)见解析；（2）平面与平面所成二面角的余弦值为.

【解析】试题分析：

由题意可证得两两垂直，建立空间直角坐标系求解．（1）通过证明，可得．（2）由题意可得平面的一个法向量为，又可求得平面的法向量为，故可求得，结合图形可得平面与平面所成的二面角为锐角，由此可得所求余弦值．

试题解析：

（1）∵平面平面平面，

∴，

又，

∴两两垂直，

以点为坐标原点， 所在直线分别为轴建立如图所示的空间直角坐标系，

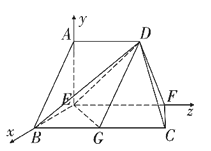
则，

∴，

∵，

∴；

（2）由已知，得是平面的一个法向量，

设平面的法向量为，

∵，

由，得，

令，得.

∴，

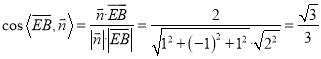由图形知，平面与平面所成的二面角为锐角，

∴平面与平面所成二面角的余弦值为．