题目内容
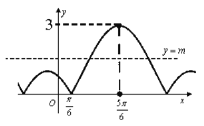
【题目】如图是函数![]() 的部分图象.
的部分图象.

(1)求函数![]() 的表达式;
的表达式;
(2)若函数![]() 满足方程
满足方程![]() ,求在
,求在![]() 内的所有实数根之和;
内的所有实数根之和;
(3)把函数![]() 的图象的周期扩大为原来的两倍,然后向右平移
的图象的周期扩大为原来的两倍,然后向右平移![]() 个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数
个单位,再把纵坐标伸长为原来的两倍,最后向上平移一个单位得到函数![]() 的图象.若对任意的
的图象.若对任意的![]() ,方程
,方程![]() 在区间
在区间![]() 上至多有一个解,求正数
上至多有一个解,求正数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)答案不唯一,具体见解析(3)
(2)答案不唯一,具体见解析(3)![]()
【解析】
(1)根据图像先确定A,再确定![]() ,代入一个特殊点再确定
,代入一个特殊点再确定![]() 。
。
(2)根据(1)的结果结合图像即可解决。
(3)根据(1)的结果以及三角函数的变换求出![]() 即可解决。
即可解决。
解:(Ⅰ)由图可知:![]() ,即
,即![]() ,
,
![]() 又由图可知:
又由图可知:![]() 是五点作图法中的第三点,
是五点作图法中的第三点,
![]() ,即
,即![]() .
.
(Ⅱ)因为![]() 的周期为
的周期为![]() ,
,![]() 在
在![]() 内恰有
内恰有![]() 个周期.
个周期.
⑴当![]() 时,方程
时,方程![]() 在
在![]() 内有
内有![]() 个实根,
个实根,
设为![]()
![]() ,结合图像知
,结合图像知![]()
![]() ,
,
故所有实数根之和为![]() ;
;
⑵当![]() 时,方程
时,方程![]() 在
在![]() 内有
内有![]() 个实根为
个实根为![]() ,
,
故所有实数根之和为![]() ;
;
⑶当![]() 时,方程
时,方程![]() 在
在![]() 内有
内有![]() 个实根,
个实根,
设为![]()
![]() ,结合图像知
,结合图像知![]()
![]() ,
,
故所有实数根之和为![]() ;
;
综上:当![]() 时,方程
时,方程![]() 所有实数根之和为
所有实数根之和为![]() ;
;
当![]() 时,方程
时,方程![]() 所有实数根之和为
所有实数根之和为![]() ;
;
(Ⅲ)![]() ,
,
函数![]() 的图象如图所示:
的图象如图所示:
则当![]() 图象伸长为原来的
图象伸长为原来的![]() 倍以上时符合题意,
倍以上时符合题意,
所以![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
【题目】某市通过随机询问100名不同年级的学生是否能做到“扶跌倒老人”,得到如下列联表:
做不到 | 能做到 | |
高年级 | 45 | 10 |
低年级 | 30 | 15 |
则下列结论正确的是( )
附参照表:
| 0.10 | 0.025 | 0.01 |
| 2.706 | 5.024 | 6.635 |
参考公式:![]() ,其中
,其中![]()
A. 在犯错误的概率不超过![]() 的前提下,认为“学生能否做到‘扶跌倒老人’与年级高低有关”
的前提下,认为“学生能否做到‘扶跌倒老人’与年级高低有关”
B. 在犯错误的概率不超过![]() 的前提下,“学生能否做到‘扶跌倒老人’与年级高低无关”
的前提下,“学生能否做到‘扶跌倒老人’与年级高低无关”
C. 有![]() 以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低有关”
以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低有关”
D. 有![]() 以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低无关”
以上的把握认为“学生能否做到‘扶跌倒老人’与年级高低无关”