题目内容
如图,△ABC中,点M是BC的中点,点N在边AC上,且AN=2NC,AM与BN相交于点P,求AP∶PM的值.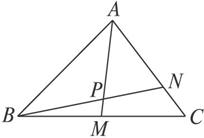
解:设
=e1,
=e2,则
=-3e2-e1,
=2e1+e2.
∵A、P、M与B、P、N分别共线,
∴存在实数λ,μ,
使
=λ
=-λe1-3λe2,
=μ
=2μe1+μe2,
故
=
-
=(λ+2μ) e1+(3λ+μ) e2,而
=
+
=2e1+3e2,
∴由平面向量基本定理得
∴
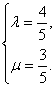
故
=
,即AP∶PM=4∶1.
练习册系列答案
相关题目
6、如图△ABC中，∠ACB=90°，直线l过点A且垂直于平面ABC，动点P∈l，当点P逐渐远离点A时，∠PCB的大小（ ）
如图△ABC中，A（0，1），B（-2，2），C（2，6）．
如图△ABC中，已知点D在BC边上，满足
,
求
；