题目内容
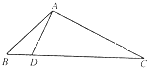 如图△ABC中,已知点D在BC边上,满足
如图△ABC中,已知点D在BC边上,满足| AD |
| AC |
2
| ||
| 3 |
| 2 |
| 3 |
(I)求AD的长;
(Ⅱ)求cosC.
分析:(I)通过向量的数量积,判断垂直关系,求出cos∠BAD的值,在△ABD中,由余弦定理求AD的长;
(Ⅱ)在△ABD中,由正弦定理,求出sin∠ADB,通过三角形是直角三角形,即可求cosC.
(Ⅱ)在△ABD中,由正弦定理,求出sin∠ADB,通过三角形是直角三角形,即可求cosC.
解答:解:(Ⅰ)∵
•
=0,
∴AD⊥AC,
∴sin∠BAC=sin(
+∠BAD)=cos∠BAD,
∵sin∠BAC=
,
∴cos∠BAD=
….(2分)
在△ABD中,由余弦定理可知BD2=AB2+AD2-2AB•ADcos∠BAD,
即AD2-8AD+15=0,
解之得AD=5或AD=3 ….(6分)
由于AB>AD,
∴AD=3…..(7分)
(Ⅱ)在△ABD中,由正弦定理可知
=
,
又由cos∠BAD=
,
可知sin∠BAD=
,
∴sin∠ADB=
=
,
∵∠ADB=∠DAC+∠C,∠DAC=
,
∴cosC=
.…(12分)
| AD |
| AC |
∴AD⊥AC,
∴sin∠BAC=sin(
| π |
| 2 |
∵sin∠BAC=
2
| ||
| 3 |
∴cos∠BAD=
2
| ||
| 3 |
在△ABD中,由余弦定理可知BD2=AB2+AD2-2AB•ADcos∠BAD,
即AD2-8AD+15=0,
解之得AD=5或AD=3 ….(6分)
由于AB>AD,
∴AD=3…..(7分)
(Ⅱ)在△ABD中,由正弦定理可知
| BD |
| sin∠BAD |
| AB |
| sin∠ADB |
又由cos∠BAD=
2
| ||
| 3 |
可知sin∠BAD=
| 1 |
| 3 |
∴sin∠ADB=
| ABsin∠BAD |
| BD |
| ||
| 3 |
∵∠ADB=∠DAC+∠C,∠DAC=
| π |
| 2 |
∴cosC=
| ||
| 3 |
点评:本题考查解三角形,余弦定理以及正弦定理的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,已知A(-3,0),B(3,0),CD⊥AB于D,△ABC的垂心为
如图,在△ABC中,已知A(-3,0),B(3,0),CD⊥AB于D,△ABC的垂心为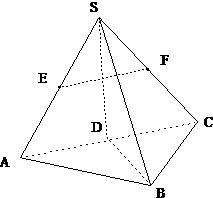 19、如图:在三棱锥S-ABC中,已知点D、E、F分别为棱AC、SA、SC的中点.
19、如图:在三棱锥S-ABC中,已知点D、E、F分别为棱AC、SA、SC的中点. 如图,三棱锥P-ABC中,已知PA⊥平面ABC,PA=3,PB=PC=BC=6,求二面角P-BC-A的正弦值.
如图,三棱锥P-ABC中,已知PA⊥平面ABC,PA=3,PB=PC=BC=6,求二面角P-BC-A的正弦值.