题目内容
1.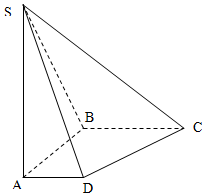 如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.
如图,在底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.(1)求四棱锥S-ABCD的体积;
(2)求证:BC⊥面SAB;
(3)求SC与底面ABCD所成角的正切值.
分析 (1),由题设条四棱锥S-ABCD的体积:V=$\frac{1}{3}$Sh=$\frac{1}{3}$×$\frac{1}{2}$×(AD+BC)×AB×SA,即可求得四棱锥S-ABCD的体积;
(2),由SA⊥面ABCD,知SA⊥BC,由AB⊥BC,BC⊥面SAB,由此能够证明面SAB⊥面SBC;
(3),连接AC,知∠SCA 就是SC与底面ABCD所成的角,由此能求出 SC与底面ABCD所成角的正切值.
解答 解:(1)∵底面是直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=$\frac{1}{2}$.
∴四棱锥S-ABCD的体积:V=$\frac{1}{3}$Sh=$\frac{1}{3}$×$\frac{1}{2}$×(AD+BC)×AB×SA=$\frac{1}{6}$×($\frac{1}{2}$+1)×1×1=$\frac{1}{4}$.
(2)证明:∵SA⊥面ABCD,BC?面ABCD,
∴SA⊥BC,
∵AB⊥BC,SA∩AB=A,
∴BC⊥面SAB.
∵BC?面SBC,
∴面SAB⊥面SBC.
(3)连接AC,
∵SA⊥面ABCD,
∴∠SCA 就是SC与底面ABCD所成的角.
在三角形SCA中,
∵SA=1,AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∴tan∠SCA=$\frac{SA}{AC}$=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$
点评 本题考查棱锥的体积公式,考查直线与平面所成角的求法,平面与平面垂直的判定定理的应用,考查空间想象能力以及计算能力,属于中档题.

练习册系列答案
相关题目
11.如图某几何体的三视图是直角边长为1的三个等腰直角三角形,则该几何体的外接球的表面积为( )
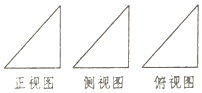

| A. | $\frac{3}{2}π$ | B. | $\sqrt{3}π$ | C. | $\frac{{\sqrt{3}}}{2}π$ | D. | 3π |
12.下列命题中错误的是( )
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | “x>5”是“x2-4x-5>0”的充分不必要条件 | |
| C. | 命题p:?x0∈R,x02+x0-1<0,则?p:?x∈R,x2+x-1≥0 | |
| D. | 命题“若x2-3x+2=0,则x=1或x=2”的逆否命题为“若x≠1且x≠2,则x2-3x+2≠0” |
9.函数f(x)=x3+4x+9的图象在x=1处的切线在x轴上的截距为( )
| A. | 7 | B. | 1 | C. | -1 | D. | -7 |
16.某赛季甲、乙两名篮球运动员每场比赛得分如图所示,则甲、乙两运动员得分的中位数分别是( )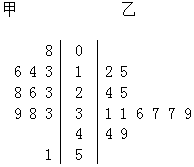

| A. | 26 33.5 | B. | 26 36 | C. | 23 31 | D. | 24.5 33.5 |