题目内容
18.已知函数f(x)=|x-2|+2|x+1|的最小值为m.(1)求m的值;
(2)若a、b、c∈R,$\frac{{a}^{2}+{b}^{2}}{2}$+c2=m,求c(a+b)的最大值.
分析 (1)讨论x的范围:x≤-1,-1<x≤2,x>2,去掉绝对值,写出分段函数的形式,画出图象即可求得m值;
(2)把m值代入$\frac{{a}^{2}+{b}^{2}}{2}$+c2=m,变形后利用基本不等式求c(a+b)的最大值.
解答 解:(1)f(x)=|x-2|+2|x+1|=$\left\{\begin{array}{l}{-3x,x≤-1}\\{x+4,-1<x≤2}\\{3x,x>2}\end{array}\right.$,其图象如图: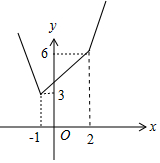
∴m=(f(x))min=3;
(2)由$\frac{{a}^{2}+{b}^{2}}{2}$+c2=m=3,得a2+b2+2c2=6.
∴c(a+b)=ac+bc≤$\frac{{a}^{2}+{c}^{2}}{2}+\frac{{b}^{2}+{c}^{2}}{2}=\frac{{a}^{2}+{b}^{2}+2{c}^{2}}{2}=\frac{6}{2}=3$.
当且仅当a=b=c时上式“=”成立.
故c(a+b)的最大值为3.
点评 本题考查分段函数的图象和性质,考查最值的求法,注意运用图象和基本不等式,考查变形和化简整理的运算能力,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
9.定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(-∞,0)∪(0,+∞)上的如下函数:(1)f(x)=x2;(2)f(x)=x2+1;$(3)f(x)=\sqrt{|x|}$;(4)f(x)=ln|x|.则其中是“保等比数列函数”f(x)的序号为( )
| A. | (1)(2) | B. | (3)(4) | C. | (1)(3) | D. | (2)(4) |
13.命题“方程x2-4=0的解是x=±2”中,使用的逻辑联结词的情况是( )
| A. | 没有使用联结词 | B. | 使用了逻辑联结词“或” | ||
| C. | 使用了逻辑联结词“且” | D. | 使用了逻辑联结词“非” |
8.设(2-x)5=a0+a1x+a2x2+…+a5x5,那么a1+a2+a3+a4+a5的值为( )
| A. | 1 | B. | -31 | C. | -32 | D. | -1 |