题目内容
【题目】设函数f(x)= 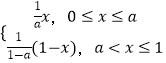 ,a为常数,且a∈(0,1).
,a为常数,且a∈(0,1).
(1)若x0满足f(x0)=x0 , 则称x0为f(x)的一阶周期点,证明函数f(x)有且只有两个一阶周期点;
(2)若x0满足f(f(x0))=x0 , 且f(x0)≠x0 , 则称x0为f(x)的二阶周期点,当a= ![]() 时,求函数f(x)的二阶周期点.
时,求函数f(x)的二阶周期点.
【答案】
(1)证明:由题可得,当0≤x≤a时, ![]() ,因为a∈(0,1),所以x=0;
,因为a∈(0,1),所以x=0;
当a<x≤1时, ![]() ,因为a∈(0,1),所以x=
,因为a∈(0,1),所以x= ![]() ,
,
所以函数f(x)有且只有两个一阶周期点.
(2)解:当 ![]() 时,
时, 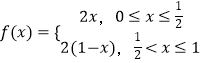
所以 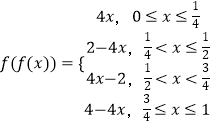
当 ![]() 时,由4x=x,解得x=0,
时,由4x=x,解得x=0,
因为f(0)=0,故x=0不是f(x)的二阶周期点;
当 ![]() 时,由2﹣4x=x,解得
时,由2﹣4x=x,解得 ![]() ,
,
因为 ![]() ,故
,故 ![]() 是f(x)的二阶周期点;
是f(x)的二阶周期点;
当 ![]() 时,由4x﹣2=x,解得
时,由4x﹣2=x,解得 ![]() ,
,
因为 ![]() ,故
,故 ![]() 不是f(x)的二阶周期点;
不是f(x)的二阶周期点;
当 ![]() 时,由4﹣4x=x,解得
时,由4﹣4x=x,解得 ![]() ,
,
因为 ![]() ,故
,故 ![]() 是f(x)的二阶周期点;
是f(x)的二阶周期点;
综上,当 ![]() 时,函数f(x)的二阶周期点为x1=
时,函数f(x)的二阶周期点为x1= ![]() ,x2=
,x2= ![]() .
.
【解析】(1)利用定义通过当0≤x≤a时,当a<x≤1时,验证函数f(x)有且只有两个一阶周期点.(2)当 ![]() 时,
时, 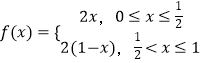 ,推出
,推出 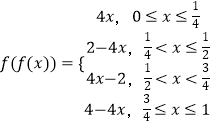 ,利用函数的定义域,通过分段求解即可.
,利用函数的定义域,通过分段求解即可.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目


