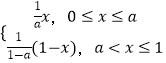题目内容
【题目】设f(x)是定义在R上恒不为零的函数,且对任意的x、y∈R都有f(x)f(y)=f(x+y),若a1= ![]() ,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
,an=f(n)(n∈N*),则数列{an}的前n项和Sn的取值范围是( )
A.[ ![]() ,1)
,1)
B.[ ![]() ,1]
,1]
C.( ![]() ,1)
,1)
D.( ![]() ,1]
,1]
【答案】A
【解析】解:∵对任意x,y∈R,都有f(x)f(y)=f(x+y), ∴令x=n,y=1,得f(n)f(1)=f(n+1),
即 ![]() =
= ![]() =f(1)=
=f(1)= ![]() ,
,
∴数列{an}是以 ![]() 为首项,以
为首项,以 ![]() 为公比的等比数列,
为公比的等比数列,
∴an=f(n)=( ![]() )n ,
)n ,
∴Sn= ![]() =1﹣(
=1﹣( ![]() )n ,
)n ,
由1﹣( ![]() )n在n∈N*上递增,可得最小值为1﹣
)n在n∈N*上递增,可得最小值为1﹣ ![]() =
= ![]() ,
,
则Sn∈[ ![]() ,1).
,1).
故选:A.
【考点精析】本题主要考查了数列的前n项和的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目
【题目】某企业节能降耗技术改造后,在生产某产品过程中几录的产量x(吨)与相应的生产能耗y(吨)的几 组对应数据如表所示:
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | a |
若根据表中数据得出y关于x的线性回归方程为 ![]() =0.7x+0.35,则表中a的值为( )
=0.7x+0.35,则表中a的值为( )
A.3
B.3.15
C.3.5
D.4.5