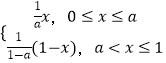Question

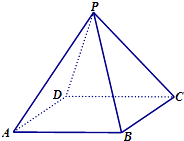
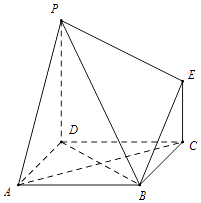
【题目】如图为一组合几何体，其底面ABCD为正方形，PD⊥平面ABCD，EC∥PD且PD=AD=2EC=2．
（I）求证：AC⊥平面PDB；
（II）求四棱锥B﹣CEPD的体积；
（III）求该组合体的表面积．

Answer 1

【答案】（Ⅰ）证明：∵PD⊥平面ABCD，∴PD⊥AC，又底面ABCD为正方形，∴AC⊥BD，
∵BD∩PD=D，
∴AC⊥平面PDB；
（Ⅱ）解：∵PD⊥平面ABCD，且PD面PDCE，
∴面PDCE⊥面ABCD，又BC⊥CD，∴BC⊥平面PDCE．
∵S梯形PDCE= （PD+EC）DC= ×3×2=3，
∴四棱锥B﹣CEPD的体积VB﹣CEPD= S梯形PDCEBC= ×3×2=2；
（Ⅲ）解：∵BE=PE= ，PB=2 ，
∴SPBE= ×2 × = ．
又∵SABCD=2×2=4，SPDCE=3，SPDA= =2，SBCE= =1，SPAB= =2 ，
∴组合体的表面积为10+2 + ．

【解析】（Ⅰ）由已知结合线面垂直的性质可得PD⊥AC，又底面ABCD为正方形，得AC⊥BD，再由线面垂直的判定得AC⊥平面PDB；（Ⅱ）由PD⊥平面ABCD，可得面PDCE⊥面ABCD，进一步得到BC⊥平面PDCE．求出S梯形PDCE ， 代入棱锥体积公式求得四棱锥B﹣CEPD的体积；（Ⅲ）求解直角三角形得△PBE的三边长，再由三角形面积公式可得组合体的表面积．
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．