题目内容

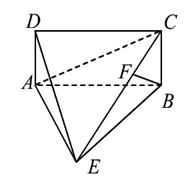
如图四棱锥E—ABCD中，底面ABCD是平行四边形。∠ABC=45°，BE=BC=   EA=EC=6，M为EC中点，平面BCE⊥平面ACE，AE⊥EB

（I）求证：AE⊥BC  （II）求四棱锥E—ABCD体积

 


（1）证明：BE=BC， M为EC中点  ∴BM⊥EC

          又平面BCE⊥平面ACE 且交于EC

          ∴BM⊥平面ACE，  AE⊥BM

          又AE⊥EB   EBBM=B    BM、EB平面BCE

     ∴AE⊥平面BCE，   AE⊥BC

   （2）设E点到平面ABCD距离为    

       

       

        

                                    

                  

       

练习册系列答案
相关题目
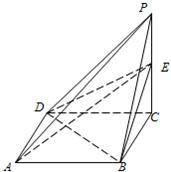19、如图四棱锥P-ABCD，PC⊥面ABCD，PC=2，面ABCD是边长为1的正方形，E是侧棱PC上的动点．
（Ⅰ） 当点E在什么位置时，AP∥面EBD？并证明；
（Ⅱ） 是否不论点E在何位置，都有BD⊥AE？证明你的结论．
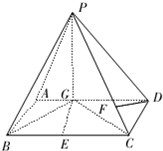已知如图四棱锥P-ABCD中，底面ABCD是平行四边形，PG⊥平面ABC，垂足G在AD上，且AG=
1
3
GD，GB⊥GC．GB=GC=2，PG=4，E是BC的中点．
（1）求证：PC⊥BG；
（2）求异面直线GE与PC所成角的余弦值；
（3）若F是PC上一点，且DF⊥GC，求
CF
CP
的值．

如图四棱锥E—ABCD中，底面ABCD是平行四边形。∠ABC=45°，BE=BC=   EA=EC=6，M为EC中点，平面BCE⊥平面ACE，AE⊥EB

（I）求证：AE⊥BC （II）求四棱锥E—ABCD体积

 

如图，四棱锥E—ABCD中，ABCD是矩形，平面EAB平面ABCD，AE=EB=BC=2，F为CE上的点，且BF平面ACE．

（1）求证：AEBE；

（2）求二面角A—CD—E的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网