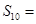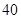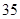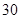题目内容
已知等差数列{an}的公差不为零,a1=25,且 ,
, ,
, 成等比数列.
成等比数列.
(Ⅰ)求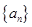 的通项公式;
的通项公式;
(Ⅱ)求 +a4+a7+…+a3n-2.
+a4+a7+…+a3n-2.
 ,
, ,
, 成等比数列.
成等比数列.(Ⅰ)求
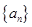 的通项公式;
的通项公式;(Ⅱ)求
 +a4+a7+…+a3n-2.
+a4+a7+…+a3n-2.(Ⅰ)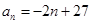 (Ⅱ)
(Ⅱ)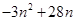
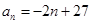 (Ⅱ)
(Ⅱ)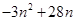
(Ⅰ)设{an}的公差为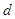 ,由题意,
,由题意,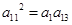 ,
,
即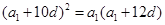 ,于是
,于是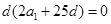 ,又a1=25,所以
,又a1=25,所以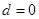 (舍去)或
(舍去)或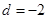 ,
,
故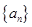 的通项公式为
的通项公式为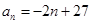 .
.
(Ⅱ)令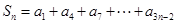 ,则由(Ⅰ)知
,则由(Ⅰ)知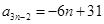 ,故
,故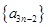 是首项为25,公差为
是首项为25,公差为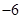 的等差数列,从而
的等差数列,从而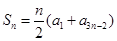 =
=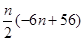 =
=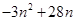 .
.
本题第(Ⅰ)问,由基本量的计算,可以得出公差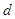 ,从而由等差数列的通项公式求出
,从而由等差数列的通项公式求出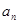 ;第(Ⅱ)问,在等差数列
;第(Ⅱ)问,在等差数列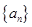 中,每隔两项拿出一项得到的新数列仍成等差数列,公式差为
中,每隔两项拿出一项得到的新数列仍成等差数列,公式差为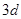 ,可以等差数列的前n项和公式求出结果.对第(Ⅰ)问,基本量的计算是高考常考的一个重点内容,注意细心计算确保正确率;准确解答第(Ⅱ)问的关键是熟练等差数列的性质以及前n项和公式.
,可以等差数列的前n项和公式求出结果.对第(Ⅰ)问,基本量的计算是高考常考的一个重点内容,注意细心计算确保正确率;准确解答第(Ⅱ)问的关键是熟练等差数列的性质以及前n项和公式.
【考点定位】本小题主要考查等差数列与等比数列的通项公式与前n项和公式,考查分析问题、解决问题的能力.
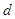 ,由题意,
,由题意,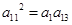 ,
,即
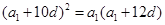 ,于是
,于是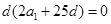 ,又a1=25,所以
,又a1=25,所以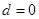 (舍去)或
(舍去)或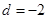 ,
,故
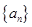 的通项公式为
的通项公式为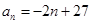 .
.(Ⅱ)令
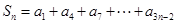 ,则由(Ⅰ)知
,则由(Ⅰ)知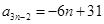 ,故
,故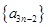 是首项为25,公差为
是首项为25,公差为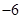 的等差数列,从而
的等差数列,从而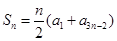 =
=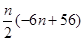 =
=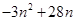 .
.本题第(Ⅰ)问,由基本量的计算,可以得出公差
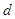 ,从而由等差数列的通项公式求出
,从而由等差数列的通项公式求出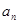 ;第(Ⅱ)问,在等差数列
;第(Ⅱ)问,在等差数列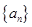 中,每隔两项拿出一项得到的新数列仍成等差数列,公式差为
中,每隔两项拿出一项得到的新数列仍成等差数列,公式差为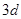 ,可以等差数列的前n项和公式求出结果.对第(Ⅰ)问,基本量的计算是高考常考的一个重点内容,注意细心计算确保正确率;准确解答第(Ⅱ)问的关键是熟练等差数列的性质以及前n项和公式.
,可以等差数列的前n项和公式求出结果.对第(Ⅰ)问,基本量的计算是高考常考的一个重点内容,注意细心计算确保正确率;准确解答第(Ⅱ)问的关键是熟练等差数列的性质以及前n项和公式.【考点定位】本小题主要考查等差数列与等比数列的通项公式与前n项和公式,考查分析问题、解决问题的能力.

练习册系列答案
相关题目
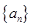 中,
中,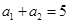 ,
,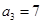 ,记数列
,记数列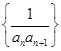 的前
的前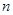 项和为
项和为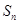 .
.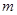 、
、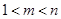 ,使得
,使得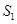 、
、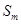 、
、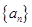 的前
的前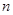 项和为
项和为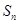 .已知
.已知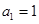 ,
,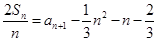 ,
,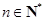 .
.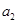 的值;
的值;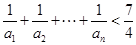 .
. 的首项
的首项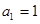 ,公比
,公比 ,等差数列
,等差数列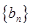 的首项
的首项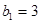 ,公差
,公差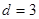 ,在
,在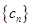 ,则
,则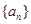 的前
的前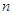 项和为
项和为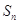 ,若
,若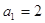 ,
,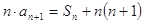 ,
,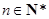 .
.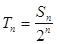 ,
,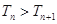 ;
;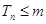 ,求
,求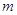 的取值范围.
的取值范围.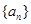 是等差数列,期中
是等差数列,期中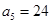 ,
,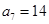
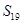
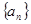 的公差
的公差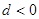 ,且
,且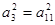 ,则该数列的前
,则该数列的前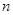 项和取得最大值时,
项和取得最大值时,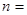
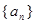 为等差数列,
为等差数列,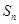 为其前
为其前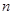 项和,
项和,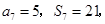 则
则