题目内容
18.已知函数f(x)=ax2-2ax+a+$\frac{1}{3}$(a>0),g(x)=bx3-2bx2+bx-$\frac{4}{27}$(b>1),则y=g[f(x)]的零点个数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 求导,确定g(x)在(0,$\frac{1}{3}$),($\frac{1}{3}$,1),(1,+∞)上分别有零点,f(x)=ax2-2ax+a+$\frac{1}{3}$=a(x-1)2+$\frac{1}{3}$≥$\frac{1}{3}$,可得f(x)在(0,$\frac{1}{3}$)上无根,在($\frac{1}{3}$,1),(1,+∞)上分别有两个根,即可得出y=g[f(x)]的零点个数.
解答 解:∵g(x)=bx3-2bx2+bx-$\frac{4}{27}$,∴g′(x)=b(3x-1)(x-1)
∴g(x)的单调增区间是(0,$\frac{1}{3}$),(1,+∞),单调减区间是($\frac{1}{3}$,1),
∵g(0)g($\frac{1}{3}$)<0,g($\frac{1}{3}$)g(1)<0,
∴g(x)在(0,$\frac{1}{3}$),($\frac{1}{3}$,1),(1,+∞)上分别有零点,
∵f(x)=ax2-2ax+a+$\frac{1}{3}$=a(x-1)2+$\frac{1}{3}$≥$\frac{1}{3}$,
∴f(x)在(0,$\frac{1}{3}$)上无根,在($\frac{1}{3}$,1),(1,+∞)上分别有两个根,
∴y=g[f(x)]的零点个数为4,
故选:B.
点评 本题考查函数的零点,考查导数知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.已知幂函数y=f(x)的图象过点$(2,\sqrt{2})$,则f(9)=( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 9 | D. | $\frac{1}{9}$ |
3.已知f(x)=x2+ax在[0,1]上是单调递减函数,则实数a的取值范围是( )
| A. | (-∞,2] | B. | (-∞,-2] | C. | [0,+∞) | D. | [2,+∞) |
10.已知$\overrightarrow a$=(3,0),$\overrightarrow b$=(-5,5)则$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{2π}{3}$ |
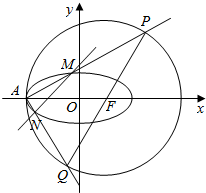 已知A(-2,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆F:(x-c)2+y2=9的一个交点,且圆心F是椭圆的一个焦点,
已知A(-2,0)是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)与圆F:(x-c)2+y2=9的一个交点,且圆心F是椭圆的一个焦点, 如图所示,在平行六面体ABCD-A1B1C1D1中,E.M.N.G分别是AA1,CD,CB,CC1的中点,求证:
如图所示,在平行六面体ABCD-A1B1C1D1中,E.M.N.G分别是AA1,CD,CB,CC1的中点,求证: