题目内容
求双曲线 的实半轴长,虚半轴长,焦点坐标,离心率,渐近线方程。
的实半轴长,虚半轴长,焦点坐标,离心率,渐近线方程。
 的实半轴长,虚半轴长,焦点坐标,离心率,渐近线方程。
的实半轴长,虚半轴长,焦点坐标,离心率,渐近线方程。实半轴长 、虚半轴长
、虚半轴长 ,焦点坐标(0,-5)(0,5),离心率
,焦点坐标(0,-5)(0,5),离心率 ,渐近线方程为
,渐近线方程为 。
。
 、虚半轴长
、虚半轴长 ,焦点坐标(0,-5)(0,5),离心率
,焦点坐标(0,-5)(0,5),离心率 ,渐近线方程为
,渐近线方程为 。
。本试题主要是考查了双曲线方程的性质的运用。求解双曲线的实半轴长,虚半轴长,焦点坐标,离心率,渐近线方程,第一要注意定位,然后利用性质进行求解

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和
和 分别是双曲线
分别是双曲线 的两个焦点,
的两个焦点, 和
和 是以
是以 为圆心,以
为圆心,以 为半径的圆与该双曲线左支的两个交点,且△
为半径的圆与该双曲线左支的两个交点,且△ 是等边三角形,则双曲线的离心率为( )
是等边三角形,则双曲线的离心率为( )



 有共同的渐近线,且过点(2, 2)的双曲线方程为
有共同的渐近线,且过点(2, 2)的双曲线方程为



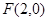 ,右顶点为
,右顶点为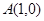 .
. 的弦
的弦 ,试求
,试求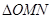 的面积(
的面积(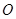 为坐标原点).
为坐标原点). 与圆
与圆 交于A、B、C、D四点,若四边形ABCD是正方形,则双曲线的离心率是 ( )
交于A、B、C、D四点,若四边形ABCD是正方形,则双曲线的离心率是 ( ) (B)
(B) (C)
(C) (D)
(D) 
 的左焦点
的左焦点 作圆
作圆 的切线,切点为
的切线,切点为 ,延长
,延长 交抛物线
交抛物线 于点
于点 ,
, 为坐标原点,若
为坐标原点,若 ,则双曲线的离心率为( )
,则双曲线的离心率为( )



 的一个焦点
的一个焦点 与抛物线
与抛物线 的焦点重合,若这两曲线的一个交点
的焦点重合,若这两曲线的一个交点 满足
满足 轴,则
轴,则 ( )
( )



 的左焦点F引圆
的左焦点F引圆 的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|—|MT|=( )
的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|—|MT|=( )


 与双曲线
与双曲线 共焦点,则椭圆C1的离心率e的取值范围为( )
共焦点,则椭圆C1的离心率e的取值范围为( )

