题目内容
在△ABC中,内角A,B,C所对的边分别为a,b,c,已知sin B(tan A+tan C)=tan Atan C.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
解:(1)证明:在△ABC中,
由于sin B(tan A+tan C)=tan Atan C,
所以sin B =
= ·
· ,
,
因此sin B(sin Acos C+cos Asin C)=
sin Asin C,
所以sin Bsin(A+C)=sin Asin C.
又A+B+C=π,所以sin(A+C)=sin B,
因此sin2B=sin Asin C.
由正弦定理得b2=ac,
即a,b,c成等比数列.
(2)因为a=1,c=2,所以b= ,
,
由余弦定理得cos B= =
=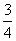 ,
,
因为0<B<π,所以sin B= =
= ,故△ABC的面积S=
,故△ABC的面积S=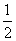 acsin B=
acsin B=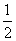 ×1×2×
×1×2× =
= .
.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 =2
=2 ,
,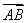 +s
+s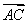 ,则r+s的值是( )
,则r+s的值是( ) B.
B.
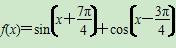 ,x∈R.
,x∈R.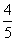 ,cos(β+α)=-
,cos(β+α)=-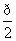 ,求证:[f(β)]2-2=0.
,求证:[f(β)]2-2=0.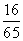 B.
B.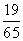 C.
C.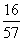 D.
D.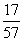
 -1)海里的B处有一艘走私船;在A处北偏西75°方向,距离A处2海里的C处的缉私船奉命以10
-1)海里的B处有一艘走私船;在A处北偏西75°方向,距离A处2海里的C处的缉私船奉命以10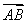 =(1,1),n=(1,-1),且n·
=(1,1),n=(1,-1),且n·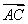 =2,则n·
=2,则n· 等于( )
等于( ) 所示,其中俯视图是中心角为
所示,其中俯视图是中心角为 的扇形,则该几何体的体积为( )
的扇形,则该几何体的体积为( ) B.
B. C.
C. D.
D.

