题目内容
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学归纳法证明你的猜想,并求出an的表达式.
解:(1)∵an=Sn-Sn-1(n≥2),
∴Sn=n2(Sn-Sn-1),∴Sn= (n≥2).
(n≥2).
∵a1=1,∴S1=a1=1.
∴S2=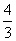 ,S3=
,S3=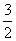 =
= ,S4=
,S4=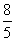 ,
,
猜想Sn=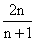 (n∈N*).
(n∈N*).
(2)证明①当n=1时,S1=1成立.
②假设n=k(k≥1,k∈N*)时,等式成立,即Sk=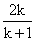 ,
,
当n=k+1时,
Sk+1=(k+1)2·ak+1=ak+1+Sk=ak+1+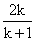 ,
,
∴ak+1=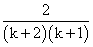 ,
,
∴Sk+1=(k+1)2·ak+1=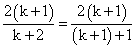 ,
,
∴n=k+1时等式也成立,得证.
∴根据①、②可知,对于任意n∈N*,等式均成立.
∴an=Sn-Sn-1=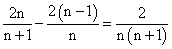 (n≥2),
(n≥2),
当n=1时,a1=1符合上式,故an=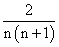 (n∈N*).
(n∈N*).

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
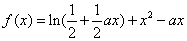 (
(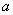 为常数,
为常数,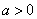 )
)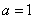 时,求函数
时,求函数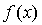 在
在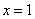 处的切线方程;(Ⅱ)当
处的切线方程;(Ⅱ)当 在
在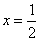 处取得极值时,若关于
处取得极值时,若关于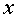 的方程
的方程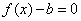 在
在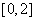 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数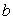 的取值范围;
的取值范围;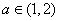 ,总存在
,总存在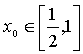 ,使不等式
,使不等式 成立,求实数
成立,求实数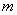 的取值范围。
的取值范围。 的二项展开式中,
的二项展开式中, 的系数为
的系数为  (B)
(B) (C)
(C) (D)
(D)
 ,则
,则 ;②
;② ;
; 为奇函数,则
为奇函数,则 ;
; ,且
,且 为周期的函数,则
为周期的函数,则 .其中正确命题是 (写出所有正确命题的编号).
.其中正确命题是 (写出所有正确命题的编号).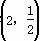 中,可以是“好点”的个数为( )
中,可以是“好点”的个数为( )