题目内容
15.已知椭圆C的焦点分别为F1($-2\sqrt{2}$,0)、F2($2\sqrt{2}$,0),长轴长为6,设直线y=x+2交椭圆C于A、B两点.(1)求椭圆的标准方程;
(2)求△OAB的面积.
分析 (1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,(a>b>0),由题意可得a,c,求得b,进而得到椭圆的方程;
(2)联立直线和椭圆方程消去y,可得x的方程,运用韦达定理和弦长公式,结合三角形的面积公式可得所求面积.
解答 解:(1)设椭圆C的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$,(a>b>0),
由题意$a=3,c=2\sqrt{2}$,于是b=$\sqrt{{a}^{2}-{c}^{2}}$=1,
所以椭圆C的方程为$\frac{x^2}{9}+{y^2}=1$;
(2)由 $\left\{{\begin{array}{l}{y=x+2}\\{\frac{x^2}{9}+{y^2}=1}\end{array}}\right.$,得10x2+36x+27=0,
由于该二次方程的△>0,所以点A、B不同.
设A(x1,y1),B(x2,y2),
则${x_1}+{x_2}=\frac{-18}{5}$,${x_1}{x_2}=\frac{27}{10}$,
方法一、设点O到直线y=x+2的距离为d,则$d=\frac{|0-0+2|}{{\sqrt{2}}}=\sqrt{2}$,
所以|AB|=$\sqrt{1+1}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}$•$\sqrt{(-\frac{18}{5})^{2}-\frac{4×27}{10}}$=$\frac{6\sqrt{3}}{5}$.
所以${S_{△AOB}}=\frac{1}{2}×\sqrt{2}×\frac{{6\sqrt{3}}}{5}=\frac{{3\sqrt{6}}}{5}$;
方法二、设直线y=x+2与x轴交于点M(-2,0),
则S△OAB=S△OAM+S△OBM,
由①可知,${y_1}+{y_2}=({x_1}+2)+({x_2}+2)={x_1}+{x_2}+4=\frac{2}{5}$,${y_1}{y_2}=({x_1}+2)({x_2}+2)={x_1}{x_2}+2({x_1}+{x_2})+4=-\frac{1}{2}$,
则${S_{△OAB}}=\frac{1}{2}•2|{y_1}|+\frac{1}{2}•2|{y_2}|=|{y_1}-{y_2}|=\sqrt{{{({y_1}-{y_2})}^2}}=\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}$
=$\sqrt{{{({\frac{2}{5}})}^2}-4({-\frac{1}{2}})}=\frac{{3\sqrt{6}}}{5}$.
点评 本题考查椭圆的方程的求法,注意运用椭圆的性质和a,b,c的关系,考查三角形的面积的求法,注意运用联立直线和椭圆方程,运用韦达定理和弦长公式,考查运算能力,属于中档题.

| A. | $\sqrt{3}$+1 | B. | $\frac{\sqrt{15}+\sqrt{3}}{2}$ | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{13}+1}{2}$ |
| A. | -6 | B. | 1 | C. | 4 | D. | 5 |
| A. | A与B互斥且为对立事件 | B. | B与C为对立事件 | ||
| C. | A与C存在着包含关系 | D. | A与C不是互斥事件 |
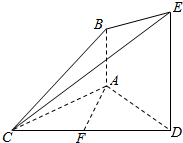 如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.