题目内容
15.下面各组函数中为相同函数的是( )| A. | $f(x)=\sqrt{{{({x-1})}^2}}\;,\;\;g(x)=x-1$ | B. | $f(x)=\sqrt{{x^2}-1}\;,\;\;g(x)=\sqrt{x+1}•\sqrt{x-1}$ | ||
| C. | $f(x)=\sqrt{\frac{1-x}{x+2}}\;,\;\;g(x)=\frac{{\sqrt{1-x}}}{{\sqrt{x+2}}}$ | D. | $f(x)={({\sqrt{x-1}})^2}\;,\;\;g(x)=\sqrt{{{({x-1})}^2}}$ |
分析 分析函数的定义域与解析式,即可得出结论.
解答 解:对于A,f(x)=|x-1|,与g(x)不是同一函数;
对于B,函数f(x)中x2-1≥0,g(x)中,x≥1,定义域不一样;
对于C,函数f(x)中$\frac{1-x}{x+2}$≥0,g(x)中,-2<x≤1,定义域一样;
对于D,定义域不一样,
故选C.
点评 本题考查函数的定义域与解析式,比较基础.

练习册系列答案
相关题目
5.已知函数f(x)=$\left\{\begin{array}{l}{lnx,x≥1}\\{1-\frac{x}{2},x<1}\end{array}\right.$,若F(x)=f[f(x)+1]+m有两个零点x1,x2,则x1+x2的取值范围是( )
| A. | [4-2ln2,+∞) | B. | [1+$\sqrt{e}$,+∞) | C. | [4-2ln2,1+$\sqrt{e}$) | D. | (-∞,1+$\sqrt{e}$) |
5.设a,b∈R,则“a>b”是“a>|b|”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
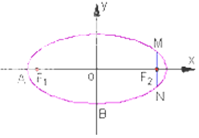 如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),b=1,左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M,N两点,且|MN|=1.
如图,在直角坐标系xOy中,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),b=1,左右两个焦点分别为F1,F2.过右焦点F2且与x轴垂直的直线与椭圆C相交M,N两点,且|MN|=1.