题目内容
【题目】已知函数![]()
(1)若曲线![]() 在x=1处的切线为y=2x-3,求实教a,b的值.
在x=1处的切线为y=2x-3,求实教a,b的值.
(2)若a=0,且![]() -2对一切正实数x值成立,求实数b的取值范围.
-2对一切正实数x值成立,求实数b的取值范围.
(3)若b=4,求函数![]() 的单调区间.
的单调区间.
【答案】(1)![]() ,
,![]() .(2)
.(2)![]() ;(3)当a=0时,
;(3)当a=0时,![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;当
;当![]() 时,
时,![]() 的增区间为
的增区间为 ,减区间为
,减区间为 ;当
;当![]() 时,
时,![]() 的增区间为
的增区间为 ,减区间为
,减区间为 ,减区间为
,减区间为 ;当
;当![]() 时
时![]() 在
在![]() 上单调递增.
上单调递增.
【解析】
(1)根据切线斜率以及函数值,得出等量关系后联立求解;
(2)采用分离参数法,构造新函数完成求解;
(3)分析导函数中![]() 的取值,采用分类的思想求解
的取值,采用分类的思想求解![]() 的单调区间.
的单调区间.
(1)![]() ,由题意知,
,由题意知,![]() ,
,![]()
解得![]() ,
,![]() .
.
(2)由题意知,![]() 恒成立,整理得
恒成立,整理得![]() 对任意
对任意![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,令
,令![]() ,解得
,解得![]() .
.
且当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,即
上单调递减,即![]()
所以![]() .
.
(3)当b=4时,![]() ,则
,则![]()
设![]()
①当a=0,![]() 的解集为
的解集为![]() ,
,![]() 的解集为
的解集为![]()
所以![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() .
.
②当![]() 时,
时,![]() 的解集为
的解集为 ,
,![]() 的解集为
的解集为
所以![]() 的增区间为
的增区间为 ,减区间为
,减区间为 .
.
③当![]() 时,
时,![]()
若![]() ,则
,则![]() ,所以
,所以![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增.
上单调递增.
若![]() ,则
,则![]() 的解集为
的解集为
![]() 的解集为
的解集为
所以![]() 的增区间为
的增区间为 ,减区间为
,减区间为 ,减区间为
,减区间为 .
.

 期末集结号系列答案
期末集结号系列答案【题目】每年春晚都是万众瞩目的时刻,这些节目体现的文化内涵、历史背景等反映了社会的进步.国家的富强,人民生活水平的提高等.某学校高三年级主任开学初为了解学生在看春晚后对节目体现的文化内涵、历史背景等是否会在今年的高考题中体现进行过思考,特地随机抽取100名高三学生(其中文科学生50,理科学生50名),进行了调查.统计数据如表所示(不完整):
“思考过” | “没有思考过” | 总计 | |
文科学生 | 40 | 10 | |
理科学生 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有![]() 的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
(2)①现从上表的”思考过”的文理科学生中按分层抽样选出7人.再从这7人中随机抽取4人,记这4人中“文科学生”的人数为![]() ,试求
,试求![]() 的分布列与数学期望;
的分布列与数学期望;
②现设计一份试卷(题目知识点来自春晚相关知识整合与变化),假设“思考过”的学生及格率为![]() ,“没有思考过”的学生的及格率为
,“没有思考过”的学生的及格率为![]() .现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
.现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
附参考公式: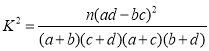 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |