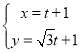题目内容
【题目】在本题中,我们把具体如下性质的函数![]() 叫做区间
叫做区间![]() 上的闭函数:①
上的闭函数:①![]() 的定义域和值域都是
的定义域和值域都是![]() ;②
;②![]() 在
在![]() 上是增函数或者减函数.
上是增函数或者减函数.
(1)若![]() 在区间
在区间![]() 上是闭函数,求常数
上是闭函数,求常数![]() 的值;
的值;
(2)找出所有形如![]() 的函数(
的函数(![]() 都是常数),使其在区间
都是常数),使其在区间![]() 上是闭函数.
上是闭函数.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)依据新定义,![]() 的定义域和值域都是
的定义域和值域都是![]() ,且
,且![]() 在
在![]() 上单调,建立方程求解;(2)依据新定义,讨论
上单调,建立方程求解;(2)依据新定义,讨论![]() 的单调性,列出方程求解即可。
的单调性,列出方程求解即可。
(1)当![]() 时,由复合函数单调性知,
时,由复合函数单调性知,![]() 在区间
在区间![]() 上是增函数,即有
上是增函数,即有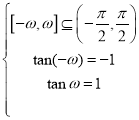 ,解得
,解得![]() ;
;
同理,当![]() 时,有
时,有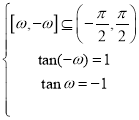 ,解得
,解得![]() ,综上,
,综上,![]() 。
。
(2)若![]() 在
在![]() 上是闭函数,则
上是闭函数,则![]() 在
在![]() 上是单调函数,
上是单调函数,
①当![]() 在
在![]() 上是单调增函数,则
上是单调增函数,则![]() ,解得
,解得![]() ,检验符合;
,检验符合;
②当![]() 在
在![]() 上是单调减函数,则
上是单调减函数,则![]() ,解得
,解得![]() ,
,
![]() 在
在![]() 上不是单调函数,不符合题意。
上不是单调函数,不符合题意。
故满足在区间![]() 上是闭函数只有
上是闭函数只有![]() 。
。

练习册系列答案
相关题目