Question

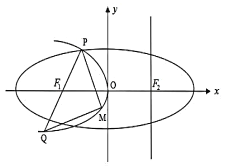
【题目】已知椭圆的焦距为4，点P（2，3）在椭圆上．

（1）求椭圆C的方程；

（2）过点P引圆的两条切线PA，PB，切线PA，PB与椭圆C的另一个交点分别为A，B，试问直线AB的斜率是否为定值？若是，求出其定值，若不是，请说明理由．

Answer 1

【答案】（1）；（2）见解析

【解析】

（1）由题可得焦点坐标，利用椭圆的定义可得，由此得到椭圆的标准方程；

（2）设出两条切线的直线方程，由切线的性质可得两切线的斜率相加0，再设出，，分别联立两切线与椭圆的方程，利用韦达定理得到，与，的关系，代入进行化简即可得到答案。

（1）椭圆C的焦距为4，所以c＝2，左焦点F1（﹣2，0），右焦点F2（2，0），

则PF1＝5，PF2＝3，所以2a＝PF1+PF2＝5+3＝8，即，则椭圆C的方程为．

（2）设PA： ，则，所以

设PB：，则，所以

所以，为方程的两根，即．

设，，联立

有，

，．

同理联立，可得：，

则．

故直线AB的斜率是定值，。