题目内容
【题目】某工厂生产甲、乙两种产品，已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额（最大供应量）如表所示：
资源 消耗量 产品 | 甲产品（每吨） | 乙产品（每吨） | 资源限额（每天） |
煤（ | 9 | 4 | 360 |
电力（ | 4 | 5 | 200 |
劳力（个） | 3 | 10 | 300 |
利润（万元） | 7 | 12 |
问：每天生产甲、乙两种产品各多少吨，获得利润总额最大？
【答案】
， 
.
【解析】试题分析：先设每天生产甲
吨，乙
吨，根据表格中煤、电力、劳动力每天资源限额列出约束条件，再根据甲、乙两种产品的利润之和建立目标函数，画出可行域，然后求得最优解，代入目标函数即求得利润的最大值和最大值时每天生产甲、乙两种产品生产的吨数.
试题解析：设此工厂应分别生产甲、乙两种产品
吨、
吨，获得利润
万元
依题意可得约束条件：
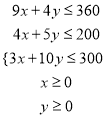
利润目标函数
，
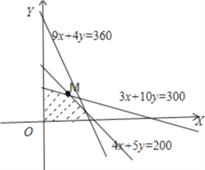
如图，作出可行域，作直线
，把直线
向右上方平移至
位置，直线经过可行域上的点
，且与原点距离最大，此时
取最大值.
解方程组
，得
故，生产甲种产品
，乙种产品
，才能使此工厂获得最大利润.
练习册系列答案
相关题目
【题目】已知函数
，则
（
）函数
定义域为__________．
（
）函数
导函数为
__________．
（
）对函数
单调研究如下
| |||||
|
|
| |||
|
____
（
）设函数
则
函数
的最大值为__________．
（5）函数
极值点共__________个，（6）其中极小值点有__________个．
（7）若关于
的方程
恰有三个不相同的实数解，则
的取值范围为__________．
