题目内容

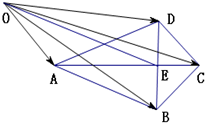已知四边形ABCD，AC是BD的垂直平分线，垂足为E，O为直线BD外一点．设向量|
OB
|=5，|
OD
|=3，则(
OA
+
OC
)•(
OB
-
OD
)的值是（　　）
分析：由已知中AC是BD的垂直平分线，垂足为E，我们根据向量加法的平行四边形潜规则可得2
OE
=
OB
+
OD
，由向量垂直数量积为0，可得
EA
•
DB
=
EC
•
DB
=0，进而可得(
OA
+
OC
)•(
OB
-
OD
)根据向量加法的三角形法则，转化为(
OB
+
OD
)•(
OB
-
OD
)，即|
OB
|2-|
OD
|2的形式，结合|
OB
|=5，|
OD
|=3，得到答案．
解答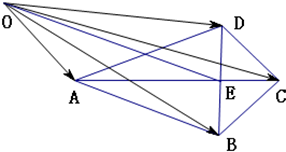：解：∵AC是BD的垂直平分线，
∴2
OE
=
OB
+
OD
，
EA
•
DB
=
EC
•
DB
=0
又∵向量|
OB
|=5，|
OD
|=3，
(
OA
+
OC
)•(
OB
-
OD
)
=(
OE
+
EA
+
OE
+
EC
)•(
OB
-
OD
)
=2
OE
•(
OB
-
OD
)+
(EA
+
EC
)•
DB

=(
OB
+
OD
)•(
OB
-
OD
)
=|
OB
|2-|
OD
|2=16
故选B
点评：本题考查的知识点是平面向量的平行四边形法则，三角形法则，及平面向量数量积的运算，其中根据已知条件得到2
OE
=
OB
+
OD
，
EA
•
DB
=
EC
•
DB
=0，是解答本题的关键．
练习册系列答案
相关题目
已知四边形ABCD，AB=AD=
2
，BC=CD=1，BC⊥CD，将四边形沿BD折起，使A′C=
3
，如图所示．
（1）求证：A′C⊥BD；
（2）求二面角D-A′B-C的余弦值的大小．
如图，已知四边形ABCD是矩形，AD⊥平面ABE，AD=AE，点F在线段DE上，且AF⊥平面BDE．求证：
（1）BE⊥平面ADE；
（2）BE∥平面AFC；
（3）平面AFC⊥平面ADE．
（2013•深圳二模）如图，已知四边形 ABCD 是矩形，AB=2BC=2，三角形 PAB 是正三角形，且 平面 ABCD⊥平面 PCD．
（1）若 O 是 CD 的中点，证明：BO⊥PA；
（2）求二面角 B-PA-D 的余弦值．
（2013•辽宁一模）如图已知四边形ABCD内接于⊙O，DA与CB的延长线交于点E，且EF∥CD，AB的延长线与EF相交于点F，FG切⊙O于点G．
求证：EF=FG．
（2013•济南二模）已知四边形ABCD是菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，G、H分别是CE、CF的中点．
（1）求证：平面AEF∥平面BDGH
（2）若平面BDGH与平面ABCD所成的角为60°，求直线CF与平面BDGH所成的角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网