题目内容
17.已知函数f(x)是R上的偶函数,它在[0,+∞)上是减函数,若f(lnx)>f(1),则x的取值范围是( )| A. | (e-1,1) | B. | (0,e-1)∪(1,+∞) | C. | (0,1)∪(e,+∞) | D. | (e-1,e) |
分析 根据题意,结合函数的奇偶性与单调性分析可得f(lnx)>f(1)⇒|lnx|<1,解可得x的取值范围,即可得答案.
解答 解:根据题意,函数f(x)是R上的偶函数,则f(lnx)=f(|lnx|),
又由在[0,+∞)上是减函数,
则f(lnx)>f(1)⇒|lnx|<1,
解可得e-1<x<e,
即x的取值范围是(e-1,e);
故选:D.
点评 本题考查函数奇偶性与单调性的综合应用,关键是得到关于x的不等式.

练习册系列答案
相关题目
7.已知向量$\overrightarrow{a}$=(1,m),$\overrightarrow{b}$=(4,-2),若$\overrightarrow{a}$$⊥\overrightarrow{b}$,则m=( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
8.执行如图的程序框图,输出的结果为( )


| A. | 57 | B. | 42 | C. | 26 | D. | 11 |
5.函数y=f(x-1)的定义域是(-1,3),则函数y=f(2x+1)的定义域为( )
| A. | (-1,7) | B. | $(-\frac{3}{2},\frac{1}{2})$ | C. | (0,4) | D. | (0,9) |
12.已知f(x)是定义在[-2,2]上的奇函数,当x∈(0,2]时,f(x)=x2-3x+4,函数y=f(x)的值域是( )
| A. | (-4,4) | B. | $(-2,-\frac{7}{4}]∪\left.{\left\{0\right.}\right\}∪[\frac{7}{4},2)$ | C. | $(-4,-\frac{7}{4}]∪\left.{\left\{0\right.}\right\}∪[\frac{7}{4},4)$ | D. | [-2,2] |
8. 已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
 已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
已知某几何体的三视图如图所示,则该几何体的外接球的表面积为( )| A. | 36π | B. | 30π | C. | 29π | D. | 20π |

 中,角
中,角 、
、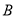 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 .
. ,求
,求 ;
;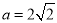 ,且
,且 的面积为
的面积为 ,求
,求 的周长.
的周长.