题目内容
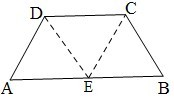
在等腰梯形ABCD中，AB∥CD，AB=2CD=8，AD=BC=5，E是AB的中点，将△ADE与△BEC分别沿边DE、CE向上折起，使A、B重合于点P，则三棱锥P-DCE的外接球的表面积为 ．
考点：球的体积和表面积,球内接多面体
专题：计算题,圆锥曲线的定义、性质与方程
分析：三棱锥P-DCE可看做一个长方体中面上的对角线构成的四面体，求出它的外接球的半径，再求表面积．
解答：
解：三棱锥P-DCE可看做一个长方体中面上的对角线构成的四面体，
设三条棱长分别为a，b，c，则a2+b2=16，c2+b2=25，a2+c2=25，
∴a2+b2+c2=33
故外接球半径为
，外接球的表面积为33π，
故答案为：33π．
解：三棱锥P-DCE可看做一个长方体中面上的对角线构成的四面体，设三条棱长分别为a，b，c，则a2+b2=16，c2+b2=25，a2+c2=25，
∴a2+b2+c2=33
故外接球半径为
| ||
| 2 |
故答案为：33π．
点评：本题考查球的内接多面体，球的表面积等知识，考查逻辑思维能力，是中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，已知在侧棱垂直于底面三棱柱ABC-A1B1C1中，AC=3，AB=5，BC=4，AA1=4，点D是AB的中点．
如图所示，在平面直角坐标系中，给定y轴正半轴上两点A（0，a），B（0，b）（a＞b＞0）．试在x轴正半轴上求一点C，试在x轴正半轴上求一点C，使∠ACB取得最大值，则C的坐标为
如图，AB切⊙O于A，D为⊙O内一点，且OD=2，连结BD交⊙O于C，BC=CD=3，AB=6，则⊙O的半径为