题目内容
已知函数f(x)=-
x2-3x+4lnx在[t,t+1]上不单调,则实数t的取值范围是 .
| 1 |
| 2 |
考点:函数的单调性与导数的关系
专题:函数的性质及应用,导数的概念及应用
分析:先由函数求f′(x)=-x-3+
,再由“函数f(x)=-
x2-3x+4lnx在[t,t+1]上不单调”转化为“f′(x)=-x-3+
=0在区间(t,t+1)上有解”从而有
=0在(t,t+1)上有解,进而转化为:x2+3x-4=0在(t,t+1)上有解,进而求出答案.
| 4 |
| x |
| 1 |
| 2 |
| 4 |
| x |
| x2+3x-4 |
| x |
解答:
解:∵函数f(x)=-
x2-3x+4lnx,
∴f′(x)=-x-3+
,
∵函数f(x)=-
x2-3x+4lnx在(t,t+1)上不单调,
∴f′(x)=-x-3+
=0在(t,t+1)上有解
∴
=0在(t,t+1)上有解
∴g(x)=x2+3x-4=0在(t,t+1)上有解,
由x2+3x-4=0得:x=1,或x=-4(舍),
∴1∈(t,t+1),
即t∈(0,1),
故实数t的取值范围是(0,1),
故答案为:(0,1).
| 1 |
| 2 |
∴f′(x)=-x-3+
| 4 |
| x |
∵函数f(x)=-
| 1 |
| 2 |
∴f′(x)=-x-3+
| 4 |
| x |
∴
| x2+3x-4 |
| x |
∴g(x)=x2+3x-4=0在(t,t+1)上有解,
由x2+3x-4=0得:x=1,或x=-4(舍),
∴1∈(t,t+1),
即t∈(0,1),
故实数t的取值范围是(0,1),
故答案为:(0,1).
点评:本题主要考查导数法研究函数的单调性,基本思路:当函数是增函数时,导数大于等于零恒成立,当函数是减函数时,导数小于等于零恒成立,然后转化为求相应函数的最值问题.注意判别式的应用.

练习册系列答案
相关题目
已知命题p:存在x0∈R,x02-x0+1<0;命题q:“x>0,a=1”是“x+
≥2”的充分不必要条件”.则下列命题正确的是( )
| a |
| x |
| A、命题“p或q”是假命题 |
| B、命题“(¬p)且q”是真命题 |
| C、命题“p或(¬q)”是真命题 |
| D、命题“(¬p)且(¬q)”是真命题 |
在△ABC中,内角A,B,C所对的边长分别是a,b,c.若c-acosB=(2a-b)cosA,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
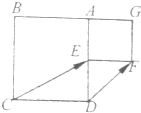 如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则
如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则