题目内容
1.已知数列{bn}的前n项和是Sn,且bn=1-2Sn,又数列{an}、{bn}满足点{an,3${b}_{n}^{2}$}在函数y=($\frac{1}{3}$)x的图象上.(1)求数列{an},{bn}的通项公式;
(2)若cn=an•bn+$\frac{1}{{b}_{n}}$,求数列{an}的前n项和Tn.
分析 (1)当n≥2时,利用bn=1-2Sn与bn-1=1-2Sn-1作差,整理得bn=$\frac{1}{3}$bn-1,进而可知数列{bn}是首项、公比均为$\frac{1}{3}$的等比数列;通过将点{an,3${b}_{n}^{2}$}代入函数解析式y=($\frac{1}{3}$)x中,进而计算可得结论;
(2)通过(1)可知cn=(2n-1)•$\frac{1}{{3}^{n}}$+3n,通过记数列{an•bn}的前n项和为Pn,数列{$\frac{1}{{b}_{n}}$}的前n项和为Qn,利用错位相减法计算可知Pn=1-(n+1)•$\frac{1}{{3}^{n}}$,利用等比数列的求和公式计算可知Qn=$\frac{{3}^{n+1}-3}{2}$,相加即得结论.
解答 解:(1)当n≥2时,bn=1-2Sn,bn-1=1-2Sn-1,
两式相减得:bn-bn-1=-2bn,即bn=$\frac{1}{3}$bn-1,
又∵b1=1-2S1,即b1=$\frac{1}{3}$,
∴数列{bn}是首项、公比均为$\frac{1}{3}$的等比数列,
∴bn=$\frac{1}{3}$•$\frac{1}{{3}^{n-1}}$=$\frac{1}{{3}^{n}}$;
∵点{an,3${b}_{n}^{2}$}在函数y=($\frac{1}{3}$)x的图象上,
∴3${{b}_{n}}^{2}$=$\frac{1}{{3}^{{a}_{n}}}$,即$\frac{1}{{3}^{2n-1}}$=$\frac{1}{{3}^{{a}_{n}}}$,
∴数列{an}的通项公式an=2n-1;
(2)由(1)可知cn=an•bn+$\frac{1}{{b}_{n}}$=(2n-1)•$\frac{1}{{3}^{n}}$+3n,
记数列{an•bn}的前n项和为Pn,数列{$\frac{1}{{b}_{n}}$}的前n项和为Qn,
∵Pn=1•$\frac{1}{3}$+3•$\frac{1}{{3}^{2}}$+…+(2n-1)•$\frac{1}{{3}^{n}}$,
$\frac{1}{3}$Pn=1•$\frac{1}{{3}^{2}}$+3•$\frac{1}{{3}^{2}}$+…+(2n-3)•$\frac{1}{{3}^{n}}$+(2n-1)•$\frac{1}{{3}^{n+1}}$,
∴$\frac{2}{3}$Pn=$\frac{1}{3}$+2($\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{3}^{n}}$)-(2n-1)•$\frac{1}{{3}^{n+1}}$
=$\frac{1}{3}$+2•$\frac{\frac{1}{{3}^{2}}(1-\frac{1}{{3}^{n-1}})}{1-\frac{1}{3}}$-(2n-1)•$\frac{1}{{3}^{n+1}}$
=$\frac{2}{3}$-$\frac{2(n+1)}{{3}^{n+1}}$,
∴Pn=1-(n+1)•$\frac{1}{{3}^{n}}$,
又∵Qn=$\frac{3(1-{3}^{n})}{1-3}$=$\frac{{3}^{n+1}-3}{2}$,
∴Tn=Pn+Qn
=1-(n+1)•$\frac{1}{{3}^{n}}$+$\frac{{3}^{n+1}-3}{2}$
=$\frac{{3}^{n+1}}{2}$-$\frac{2(n+1)}{{3}^{n}}$-$\frac{1}{2}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,考查分组法求和,考查运算求解能力,注意解题方法的积累,属于中档题.

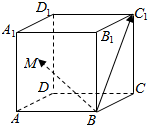 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点M是左侧面ADD1A1上的一个动点,满足$\overrightarrow{B{C}_{1}}$•$\overrightarrow{BM}$=1,则$\overrightarrow{B{C}_{1}}$与$\overrightarrow{BM}$的夹角的最大值为( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点M是左侧面ADD1A1上的一个动点,满足$\overrightarrow{B{C}_{1}}$•$\overrightarrow{BM}$=1,则$\overrightarrow{B{C}_{1}}$与$\overrightarrow{BM}$的夹角的最大值为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
| A. | (-2,1] | B. | [-2,1) | C. | [-2,1] | D. | [1,2] |
| A. | y=cos(2x+$\frac{5π}{12}$) | B. | y=-sin2x | C. | y=cos(2x+$\frac{π}{4}$) | D. | y=sin2x |