题目内容
 如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2| 2 |
分析:旋转后的几何体是圆台除去一个倒放的圆锥,根据题目所给数据,求出圆台的侧面积、圆锥的侧面积、圆台的底面积,即可求出几何体的表面积.求出圆台体积减去圆锥体积,即可得到几何体的体积.
解答: 解:四边形ABCD绕AD旋转一周所成的
解:四边形ABCD绕AD旋转一周所成的
几何体,如右图:
S表面=S圆台下底面+S圆台侧面+S圆锥侧面
=πr22+π(r1+r2)l2+πr1l1
=π×52+π×(2+5)×5+π×2×2
=25π+35π+4
π
=60π+4
π.
体积V=V圆台-V圆锥
=
[25π+
+4π]×4-
×2π×2×2
=
×39π×4-
×8π
=
.
所求表面积为:60π+4
π,体积为:
.
 解:四边形ABCD绕AD旋转一周所成的
解:四边形ABCD绕AD旋转一周所成的几何体,如右图:
S表面=S圆台下底面+S圆台侧面+S圆锥侧面
=πr22+π(r1+r2)l2+πr1l1
=π×52+π×(2+5)×5+π×2×2
| 2 |
=25π+35π+4
| 2 |
=60π+4
| 2 |
体积V=V圆台-V圆锥
=
| 1 |
| 3 |
| 25π×4π |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 148π |
| 3 |
所求表面积为:60π+4
| 2 |
| 148π |
| 3 |
点评:本题是基础题,考查旋转体的表面积与体积,转化思想的应用,计算能力的考查,都是为本题设置的障碍,仔细分析旋转体的结构特征,为顺利解题创造依据.

练习册系列答案
相关题目
 如图,在四边形ABCD中,△ABC为边长等于
如图,在四边形ABCD中,△ABC为边长等于 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=7,AD=6,S△ADC= 如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=60°,AC=6,AD=5,S△ADC=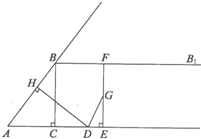 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BBl∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒. (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,