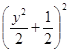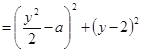Question

【题目】“”是“对任意的正数， ”的（ ）

A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件

【答案】A

【解析】分析：根据基本不等式，我们可以判断出“”?“对任意的正数x，2x+≥1”与“对任意的正数x，2x+≥1”?“a=

”真假，进而根据充要条件的定义，即可得到结论．

解答：解：当“a=”时，由基本不等式可得：

“对任意的正数x，2x+≥1”一定成立，

即“a=”?“对任意的正数x，2x+≥1”为真命题；

而“对任意的正数x，2x+≥1的”时，可得“a≥”

即“对任意的正数x，2x+≥1”?“a=”为假命题；

故“a=”是“对任意的正数x，2x+≥1的”充分不必要条件

故选A

【题型】单选题
【结束】
11

【题目】如图，四棱锥中， 平面，底面为直角梯形， ， ， ，点在棱上，且，则平面与平面的夹角的余弦值为（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】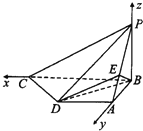

以B为坐标原点,分别以BC、BA、BP所在直线为x、y、z轴,

建立空间直角坐标系，

则，

∴

设平面BED的一个法向量为，

则，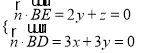

取z=1,得，

平面ABE的法向量为，

∴.

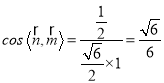∴平面ABE与平面BED的夹角的余弦值为.

故选B.