题目内容
3.设A,B是抛物线y=x2上两点,O是坐标原点,若OA⊥OB,则下列结论正确的有①②③④①|OA|•|OB|≥2;②|OA|+|OB|≥2$\sqrt{2}$;
③直线AB过抛物线y=x2的焦点;④O到直线AB的距离小于或等于1.
分析 设直线AB方程为y=kx+b,将直线AB方程代入抛物线方程y=x2,利用韦达定理,结合直线垂直的条件,能够证明直线AB过定点,即可判断结论.
解答 解:设直线AB方程为y=kx+b,A(x1,y1),B(x2,y2),
将直线AB方程代入抛物线方程y=x2,
得x2-kx-b=0,
则x1+x2=k,x1x2=-b,
∵OA⊥OB,∴kOA•kOB=-b=-1,b=1.
于是直线AB方程为y=kx+1,该直线过定点(0,1).故③正确;
O到直线AB的距离d=$\frac{1}{\sqrt{{k}^{2}+1}}$≤1,即④正确;
当k=0时,|OA||OB|取得最小值2,∴①|OA|•|OB|≥2正确;②由基本不等式,可得|OA|+|OB|≥2$\sqrt{2}$正确.
故答案为①②③④.
点评 本题考查直线过定点的证明,考查直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.设实数x、y满足约束条件$\left\{\begin{array}{l}{y-2x≤0}\\{2x+y≤6}\\{y≥\frac{1}{2}}\end{array}\right.$,则2x+$\frac{1}{y}$的最小值为( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | $\frac{10}{3}$ | D. | $\frac{3}{2}$ |
12.在直角△ABC中,AD为斜边BC边上的高,则下列结论错误的是( )
| A. | $\overrightarrow{AD}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=0 | B. | |$\overrightarrow{AB}$+$\overrightarrow{AC}$|≥2|$\overrightarrow{AD}$| | C. | $\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|2 | D. | $\overrightarrow{AC}$•$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$=|$\overrightarrow{AB}$|sinB |
12.设复数z1=-1+2i,z2=2+i,其中i为虚数单位,则z1•z2=( )
| A. | -4 | B. | 3i | C. | -3+4i | D. | -4+3i |
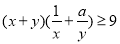 对任意正实数
对任意正实数 恒成立,则正实数
恒成立,则正实数 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.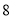
 ,
, ,
, ,则向量
,则向量 在向量
在向量 方向上的投影是________.
方向上的投影是________.