题目内容
设椭圆
+y2=1的左、右焦点分别为F1,F2,M为椭圆上异于长轴端点的一点,∠F1MF2=2θ,△MF1F2的内心为I,
则|MI|cosθ= .
| x2 |
| 4 |
则|MI|cosθ=
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:运用椭圆的定义和圆的切线的性质及内心的定义,结合解直角三角形的知识,即可求得.
解答:
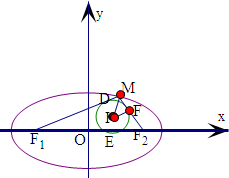 解:设△MF1F2的内切圆与△MF1F2相切于D,E,F,
解:设△MF1F2的内切圆与△MF1F2相切于D,E,F,
设MD=u,DF1=v,FF2=t,
则MD=MF=u,DF1=EF1=v,EF2=FF2=t,
由椭圆的定义,可得,MF1+MF2=2a=4,F1F2=2c=2
,
即有2u+v+t=4,v+t=2
,即有2u=4-2
,
即u=2-
,
再由|MI|cosθ=MF=u=2-
.
故答案为:2-
.
 解:设△MF1F2的内切圆与△MF1F2相切于D,E,F,
解:设△MF1F2的内切圆与△MF1F2相切于D,E,F,设MD=u,DF1=v,FF2=t,
则MD=MF=u,DF1=EF1=v,EF2=FF2=t,
由椭圆的定义,可得,MF1+MF2=2a=4,F1F2=2c=2
| 3 |
即有2u+v+t=4,v+t=2
| 3 |
| 3 |
即u=2-
| 3 |
再由|MI|cosθ=MF=u=2-
| 3 |
故答案为:2-
| 3 |
点评:本题考查椭圆的方程和定义,考查切线的性质和内心的定义,以及解直角三角形的知识,属于中档题.

练习册系列答案
相关题目
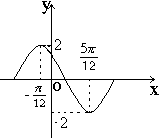 函数y=Acos(ωx+φ)在一个周期内的图象如下,此函数的解析式为( )
函数y=Acos(ωx+φ)在一个周期内的图象如下,此函数的解析式为( )A、y=2cos(2x+
| ||||
B、y=2cos(2x-
| ||||
C、y=2cos(
| ||||
D、y=2cos(2x+
|
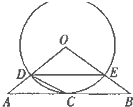 如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.