题目内容
已知:0<a<b<c<d 且a+d=b+c,求证: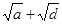 <
< 
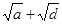 <
< 
见解析
试题分析:
直接证明显然不容易入手,所以采用分析法证明,从要证明的不等式出发,寻找使这个不等式成立的某一"充分的"条件,为此逐步往前追溯(执果索因),一直追溯到已知条件或一些真命题为止.
根据题意可知,
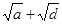 和
和 都是正数,所以为了证明结论,给不等式两边同时平方,而后根据题意
都是正数,所以为了证明结论,给不等式两边同时平方,而后根据题意 ,只需证明
,只需证明 ,将其平方,可得
,将其平方,可得 .由于不等式中含有四个未知数,所以可利用其中三个将另一个表示出来,不妨消掉
.由于不等式中含有四个未知数,所以可利用其中三个将另一个表示出来,不妨消掉 ,即
,即 ,带入
,带入 ,化简可得
,化简可得 ,根据题意,
,根据题意, ,该不等式显然成立.所以该不等式得证.
,该不等式显然成立.所以该不等式得证.试题解析:因为
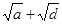 和
和 都是正数,
都是正数,所以为了证明
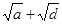 <
<
只需证

只需证

而

即证

即证

又
 所以
所以
即证:

即证:

即证:

而

所以
 显然成立
显然成立所以原不等式成立。

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 的不等式
的不等式 (
( )的解集为
)的解集为 ,且
,且 ,则
,则 ( )
( )



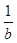 -
-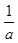 =1,则a-b<1;
=1,则a-b<1;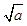 -
-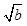 |=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.
|=1,则|a-b|<1;④若|a3-b3|=1,则|a-b|<1.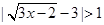 (2)
(2)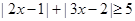
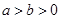 ,
,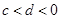 ,则一定有( )
,则一定有( )



 ;
; +
+ )≥4;
)≥4; ≥a+b;
≥a+b; ≥-2.
≥-2. 则
则 的大小关系为
的大小关系为


